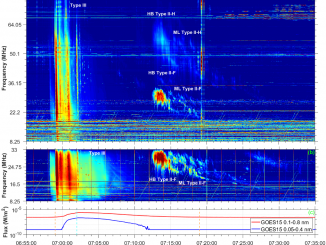
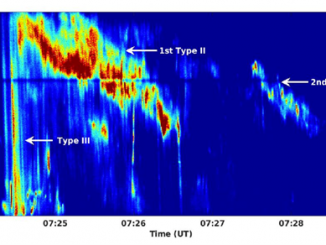
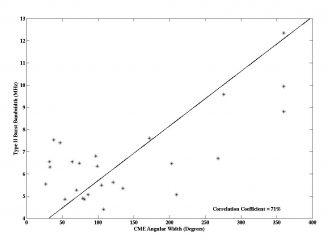
Morphology of solar type II bursts caused by shock propagation through turbulent and inhomogeneous coronal plasma by A. Koval et al
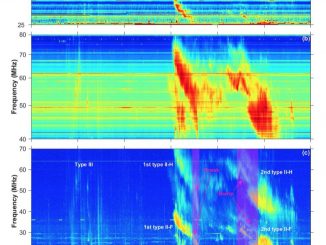
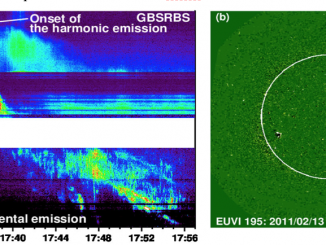
Type II solar bursts are radio signatures of shock waves in the solar corona driven by solar flares or coronal mass ejections. Therefore, these bursts present complex spectral morphologies in solar dynamic spectra. In particular, the radio emission lane may separate into two thinner bands that is known as band-splitting (Vršnak et al., 2002). “Fractured” type II bursts, exhibiting spectrally indented shapes in the form of bumps or breaks, are […]