Fermi (1949) introduced a fundamental stochastic process to solve the problem of particle energization (heating and/or acceleration) in space and astrophysical plasmas. The initial idea of Fermi with randomly moving scatterers (magnetic clouds), was soon replaced with a spectrum of low amplitude (δΒ/Β<<1) waves and termed particle acceleration by MHD (weak) turbulence. In the other extreme, isolated turbulent shock waves or isolated unstable current sheets (UCS) were studied. The regime of strong MHD turbulence (δΒ/Β ~ 1) was left unexplored for many years. This regime is now called “turbulent reconnection”, since fragmentation and the random appearance of UCSs is one of its main characteristics. The comparison of the old concept of Fermi with the new concept of turbulent reconnection is relatively easy if we replace the original magnetic clouds with an ensemble of UCS. A difficult task in the replacement is the estimate of the transport coefficients and the assessment of the validity of the Fokker-Planck (FP) equation. In order to explore these concepts, we constructed a simple numerical scheme, namely a random walk model on a lattice, as illustrated in the figure below:
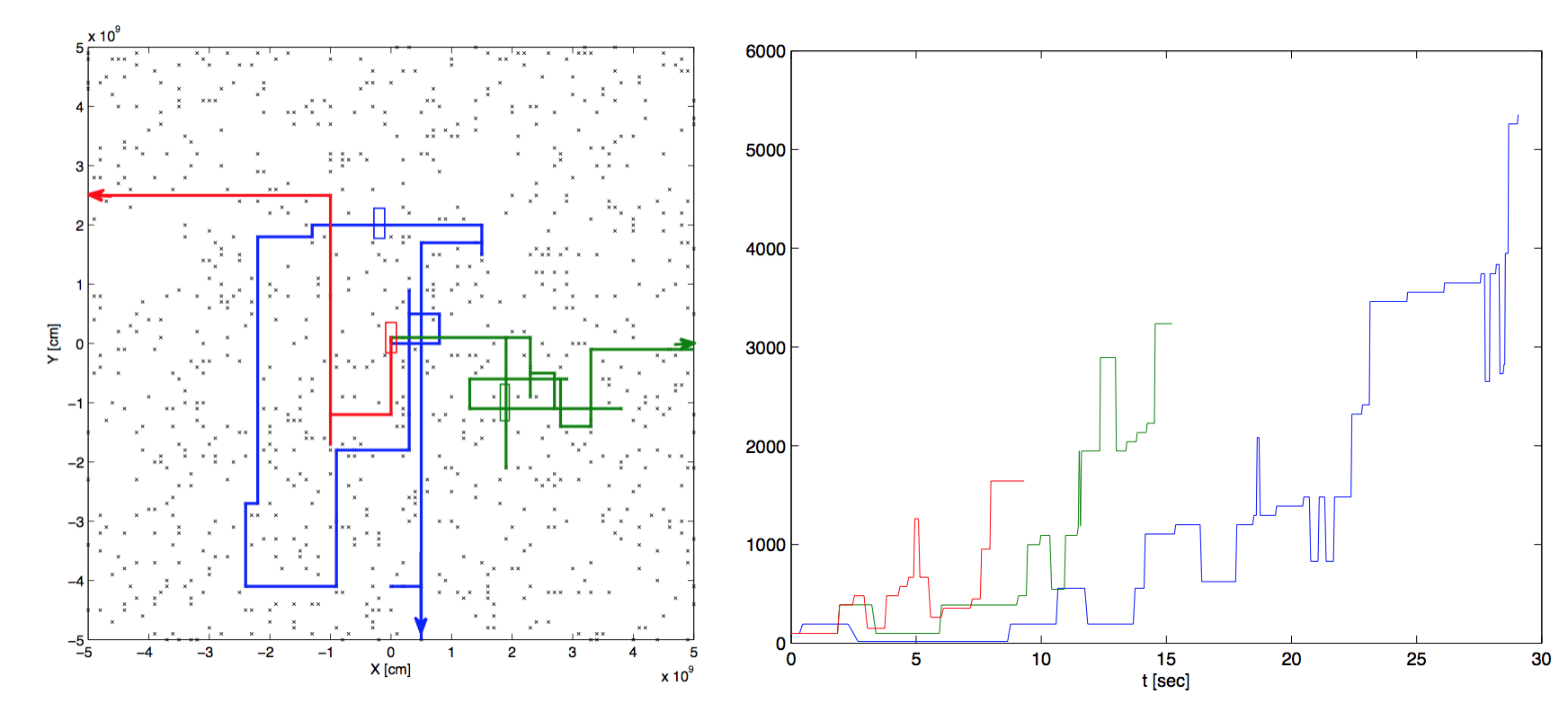
Figure 1: (a) Typical trajectories of particles inside the grid with linear dimension L=1010 cm. With black dots we have marked the active scatterers. The particles move along a straight path till they encounter a scatterer, where they are energized, and then they move into a new random direction. (b) The kinetic energy of three randomly chosen particles as a function of time.
Stochastic Fermi acceleration
Using the old concept of Fermi with magnetic clouds, we have recovered most of the characteristics of the original concept (see Figure 2), and we also have proven the validity of the FP equation (yet with transport coefficients different from the ones proposed by Fermi).
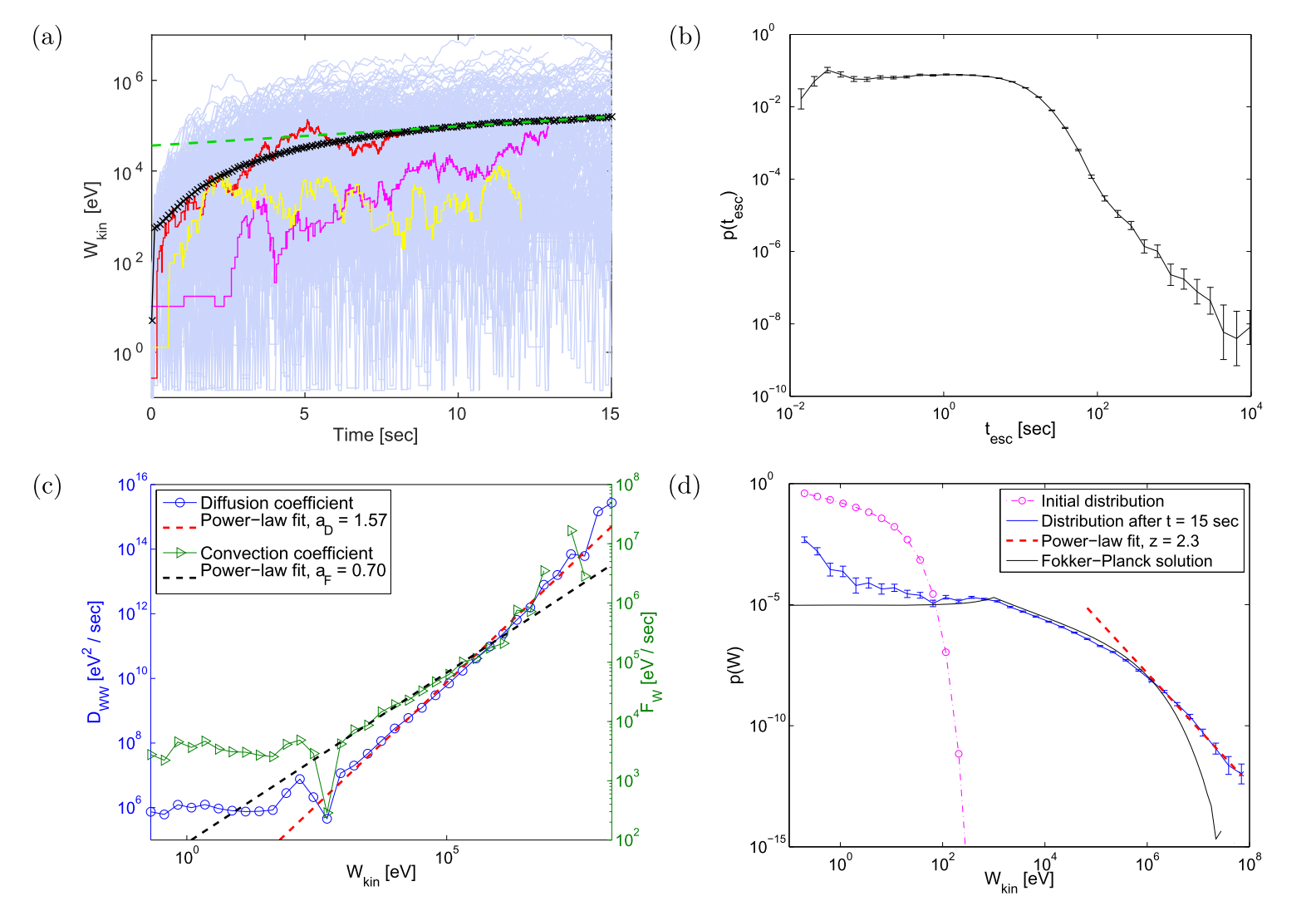 Figure 2: (a) Mean energy increase as a function of time and the energy evolution of typical particles. (b) The escape time distribution. (c) The energy diffusion and convection coefficients as a function of the kinetic energy. (d) Energy distribution at t=0 sec and t=15 sec, together with the solution of the FP equation at final time.
Figure 2: (a) Mean energy increase as a function of time and the energy evolution of typical particles. (b) The escape time distribution. (c) The energy diffusion and convection coefficients as a function of the kinetic energy. (d) Energy distribution at t=0 sec and t=15 sec, together with the solution of the FP equation at final time.
Turbulent reconnection
Our next step was to replace the magnetic clouds with UCS and to explore the new accelerator, which has many similarities with the old concept and important differences, see Fig. 3. For instance, the diffusion coefficient is now vanishing, and the FP equation yields only heating and cannot reproduce the energy distribution of the particles. Thus, newer tools, which allow for anomalous transport, are needed for the kinetic modelling of acceleration in turbulent reconnection.
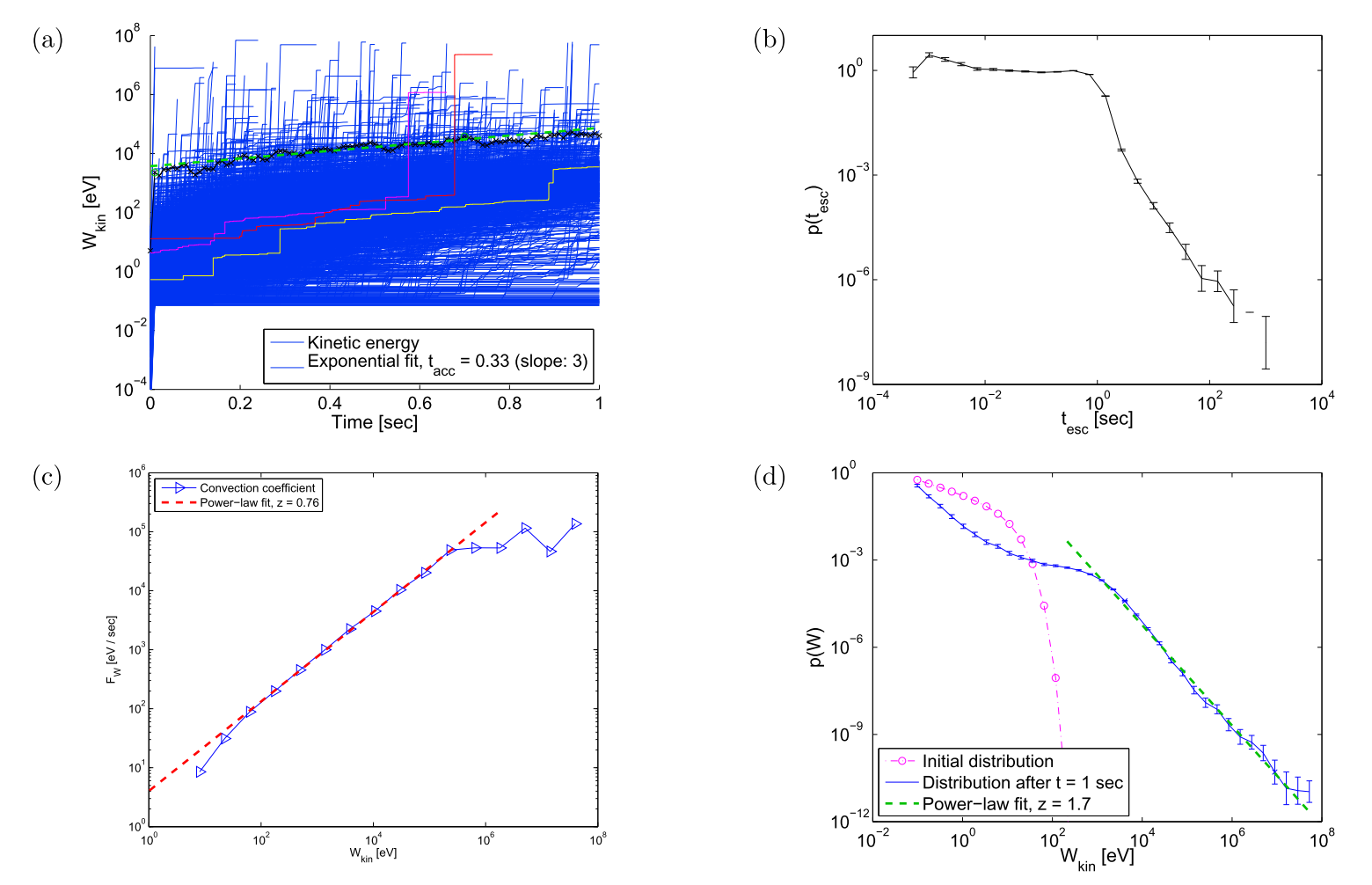
Figure 3: (a) The mean energy increase as a function of time and the energy evolution of some typical particles are shown. (b) The escape time distribution of the particles. (c) The energy convection coefficient as a function of the kinetic energy. (d) Initial and final (asymptotic) kinetic energy distribution.
In a recent article, all these concepts are presented and analysed in detail (in press at Astroph. J. Lett., 2016, see also http://arxiv.org/abs/1604.05234 ).
References
Fermi, E., 1949, Physical Review, 75, 1169
Vlahos, L., Pisokas, T., Isliker, H., Tsiolis, V. and Anastasiadis A., 2016, Astrophysical Journal Letters (in press)
