We suggest a new method for the analysis of fine structures in the cosmic plasma and investigate its applicability for the diagnostics of the solar atmosphere on scales that are not accessible by current observational techniques. The method is based on coherent interaction (diffraction) of radio waves with regular structures – as an example one can consider plasma waves of various kinds, periodic oscillations in the shock-fronts, or even stationary structures like coronal loops that have at least quasi-periodic spatial distribution of plasma parameters.
Principles
The method is new in the context of plasma physics (not only solar!), but its principles can be easily illustrated by analogy with the structural analysis used in X-ray crystallography. A well known diffraction effect is observed in crystallography when a crystal irradiated by continuous X-ray emission reflects only radiation of certain frequency and its multiples in a given direction. We expect – by analogy – strong frequency dependence of the intensity of the transmitted and reflected radio radiation passing through a regular coronal structure. As a consequence, we should observe radio emission with a frequency pattern – a component with regular modulation in the frequency, superimposed over radio continuum.
Model
Propagation of the electromagnetic (radio) wave, as described by the electric field intensity \( E(r,t) \) in unmagnetised stationary inhomogeneous plasmas (notice the spatial dependence of plasma frequency) is governed by the equation
\begin{equation} \frac{\partial^2 E(r,t)}{\partial t^2}
-c^2\Delta E(r,t)+\omega ^2_p(r) E(r,t)=0, \tag{1}\end{equation}
where \(\omega_p(r)\) is the plasma frequency. In order to study the possibility of expected selective frequency filtering on coronal fine structures we analysed the propagation of a radio wave in the plasma perturbed by 1D finite periodic sequence of electron density heaps and wells. As coherence is essential for diffraction effects we had to use the wave optics approach in solving directly Eq. (1). The analytical solution is, however, possible only for a limited number of cases of spatial density/plasma frequency distributions. We have chosen a series of square-shaped density wells (Fig. 1) in a homogeneous background, because for such a case the solution of Eq. (1) can be obtained analytically using the mode-matching technique well known from the wave-guide theory or quantum mechanics.
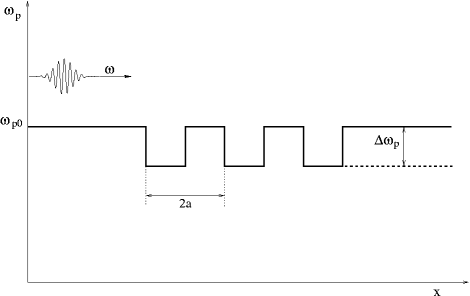
Fig 1: The 1D electron density structure (expressed in the scale of the corresponding plasma frequency) in the form of a finite series of periodically repeating square-shaped wells of depth Δωp and of period 2a. An electromagnetic wave with the angular frequency ω>ωp0 comes from the left and is partly transmitted and partly reflected. Two cases were studied: background density is homogeneous (solid line) and background density drops by Δωp behind the structure (dashed line).
As a result, we obtained transmission and reflection coefficients that depend on the frequency of the incident wave. Due to the frequency dependence of the transmission (or reflection) coefficient, the observed spectrum of radiation received after the transmission (reflection) must be affected by the density structure.
Example: the zebra pattern
As an example we present here the modelled spectrum of received radio flux, which was formed by transmitting a broad-band Gaussian-shaped radio emission with the frequency bandwidth of ~200 MHz, on a single density well of period 2a=8m with the relative depth of 23% of the background plasma frequency (Fig. 2). The spectrum exhibits regular modulation in frequency, which is a typical feature of the zebra pattern observed time to time by radio spectrographs (Fig. 3).
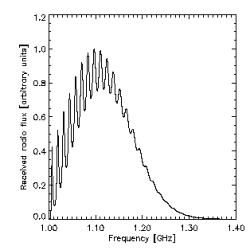
Fig 2: Spectrum of the broad-band continuum emission of the originally Gaussian spectral profile after the filtration via transmission through the single density well. See text for parameters.
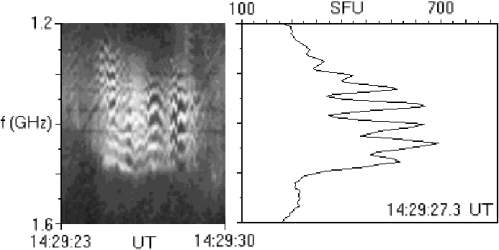
Fig 3: The zebra pattern observed on May 2, 1998 in the decimetric range by the Ondrejov radiospectrograph. The dynamic spectrum (left) and frequency profile at 14:29:27.3 UT (right) are shown.
In view of these results, we suggest that at least some observed zebra patterns can be caused by the above studied coherent propagation effects (the diffraction). The fact that the fine coronal structures leave their traces on the spectrum of transmitted radio emission is significant for diagnostics of such structures. We suggest that the zebra patterns may be used for radio diagnostics of fine coronal structures in a very similar way as the X-ray diffraction patterns (Fig. 4) are used for the structural analysis of materials, even for those exhibiting non-strict periodicity (a feature typical for plasma structures) – e.g. glasses or organic matter.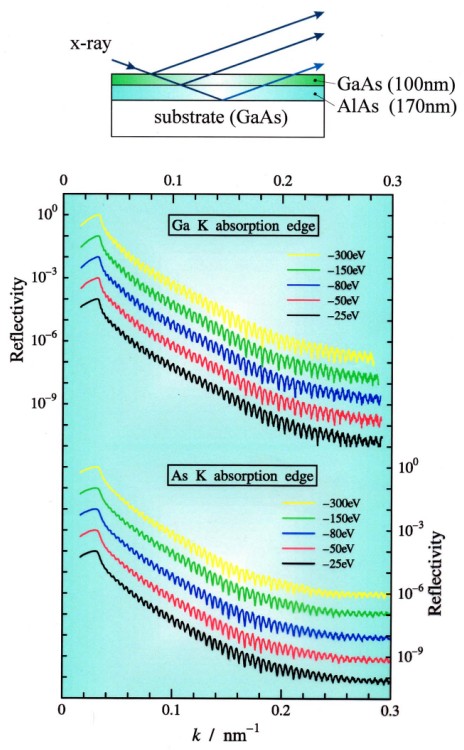
Fig 4: The X-ray reflection coefficient for GaAS/AlAs substrate dependent on the wave number.
Discussion: the fine coronal structures
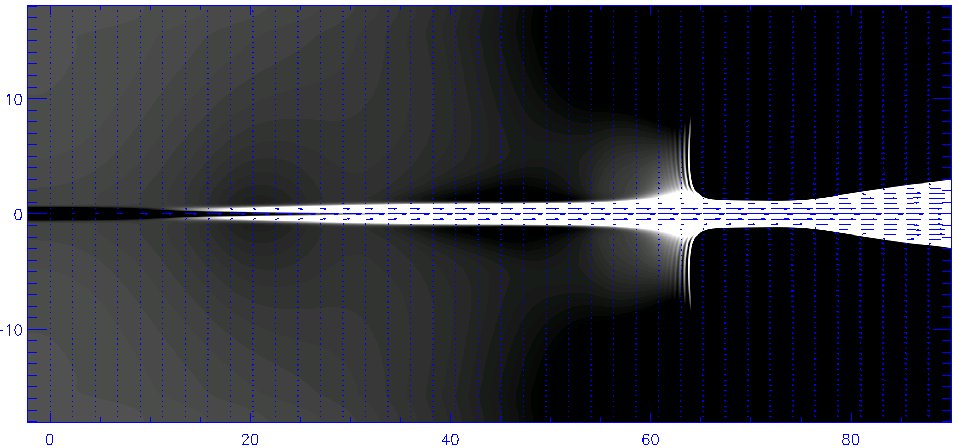
The well known statement of the diffraction theory says that the local wavelength of the diffracting waves has to be comparable with the period of regular structures the wave interacts with. In the case of the proposed radio “structural analysis” the fine coronal structures which can influence the spectrum by the above described mechanism should fall into the size range of meters to tens of meters. Besides other possibilities, we would like to mention the quasi-periodic oscillations in the shock fronts, predicted already by Sagdeev. Since according to both the theory and observations their periods are comparable to the ion inertial length, they fit well with the scales required for the radio wave diffraction. An example of the shock front generated during our 2D MHD simulation of the magnetic reconnection is shown in Fig. 5.
 |
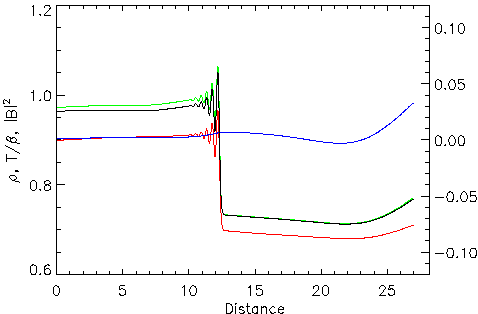 |
Fig. 5: The ion-sound shock propagating inside the 2D reconnection box (left; displayed quantities: the plasma density in grayscale, white means enhanced density, and velocity field as blue arrows) and its profile (right). The period of visible front oscillations corresponds to the ion inertial scale (meters to tens of meters in coronal conditions).
To conclude, we believe that even such small (tens of meters), yet non-resolved structures are present in the solar corona and that they may be analysed using radio waves in a similar way as the X-rays are used in crystallography – the only difference is in the spatial scale.
Retrieve the full paper by Bárta, M., Karlický, M.: Astron. Astrophys. 450, 359, 2006
