Investigating the generation mechanism for the stripes-pattern radio spectra is important to understand the dynamics of non-thermal electrons in several astronomical objects, including the Sun, Jupiter, and the Crab Pulsar. A new analytical study is carried out to identify the plasma characteristics of fiber- and zebra-pattern emission sources without an underlying density or magnetic model. The study suggests that the plasma condition of the source region for zebra pattern emission is $\omega_c < \omega_p < k_\perp v_\perp $ where $s$ is the ratio of the instability growth rate $ k_\perp v_\perp$ to the electron gyrofrequency $\omega_c$ and $\omega_p$ is the plasma frequency. While the plasma condition for the fiber radio burst is $k_\perp v_\perp < \omega_p < \omega_c$. That indicate the magnetic field strength of the source regions of fiber radio bursts is relatively stronger than the magnetic field strength of the source regions of zebra pattern radio emissions. The latter emission occurs before the recovery of magnetic field near the magnetic reconnection point.

Properties of the source region of striped emission

The source region of the stripes emission is mostly located underneath the reconnection point X-point (see Figure 1), where the ratio s of the instability growth rate to the electron gyrofrequency $\omega_c$ does not equal unity, i.e. $s=k_\perp v_\perp/ \omega_c \neq 1$. The general relation between the electron gyrofrequency $\omega_c$ and the rate
$k_\perp v_{\perp, max}$ is
$$
k_\perp v_{\perp, max} \approx s \omega_c \tag{1}
\label{eq:har_num_gen},
$$
where $ s \in \mathbb{R}$ is a real number and it represents the harmonic number H between $\omega_c$ and $k_\perp v_{\perp, max}$. When $|s|= (1/H) <1$ the plasma condition of the source region becomes $k_\perp v_\perp < \omega_p < \omega_c$ and the emission source is likely to produce a fiber radio burst. For $|s|= H >1$ the plasma condition of the source region is $\omega_c < \omega_p < k_\perp v_\perp $ and the emission source is likely to produce zebra-pattern emission. The kinetic instability rate could be expressed as
$$
k_\perp^2 v_{\perp, max}^2 =\frac{s^2}{s^2-1} \frac{e^2 N_e}{m_e \epsilon_0}  = \frac{s^2}{s^2-1} \left[\frac{e}{m_e} (\nabla \cdot E)\right]\,,
$$
where $(\nabla \cdot E)$ is the electric field $E$ divergence that represents the rate of changing the electron density, perpendicular to the magnetic field lines, in the cross-section area underneath the X-point. The weight $\mathrm{S}_R=s^2/(s^2-1)$ is the ratio of the squared kinetic instability rate $\text{k}_\perp^2 v_\perp^2$ to the term $(e/m_e) \nabla \cdot E$ , where the latter represents the local electric charge in the cross-sectional area near the X-point. Figure 2 shows the variation of $\mathrm{S}_R$ with $s$ for the cases of $s>1$ and $s<1$. It shows that $\mathrm{S}_R$ is not defined when $s$→$1$, which means, according to the condition $k_\perp v_{\perp, max} \approx s \omega_c$, that $k_\perp v_{perp, max}$ and $\omega_c $ are in resonance, and that almost happens early of the magnetic reconnection process. Subsequently, the latter process produces accelerated particles, causes an instability that propagates inwards or outwards the magnetic field loop underneath the X-point. See the link for more details.

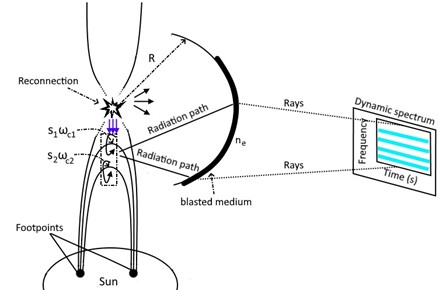
Figure 1. Proposed schema of formatting a stripes-pattern dynamic spectrum after it is generated in the region underneath the magnetic X-point and passed through the blasted medium surrounding the X-point. The density $n_e$ on the ahead surface of the blast wave plays an important role in determining the critical frequency for transmitting the radiation. The emission received by the observer would be a portion of the whole radio emission that was produced at the source.

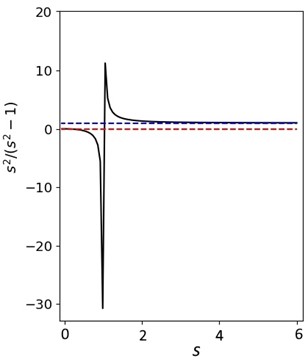
Figure 2. Variation of $s^2/(s^2− 1) = $\mathrm{S}_R$ with s. The value of $\mathrm{S}_R$ at $s=1$ is not defined ($\infty$). The horizontal blue dashed line is located at $\mathrm{S}_R$ = 1 and the red dashed line is located at $\mathrm{S}_R$ = 0.

 

Kinematics of the transmitting medium of radio waves: a case study

The study has been extended to describe the kinematics of the transmitting medium of radio waves. An approach is applied to estimate the plasma parameters of a zebra-pattern emission source observed on 2011 June 21. The medium of the radio emission pass, which is accelerated by magnetic reconnection, seems to propagate as a sausage-like wave and expands isothermally from the reconnection/source point into the solar atmosphere.

Conclusion

The study clarifies that the stripes emissions (such as fiber bursts and zebra pattern radio emission) are generated by the same mechanism, but the spectrum is obtained as fiber radio burst when the ratio $s \approx \text{k}_\perp v_\perp/\omega_c < 1$ and the plasma frequency of the emission source attributes as $\omega_p < \omega_c$. On the contrary, the plasma conditions of zebra pattern radio emission source are $s >1$ and $\omega_p > \omega_c$. The analytical study is proposed to provide a method for investigating the evolution of the stripes pattern radio sources without underlying distribution models that may be important to approach the real properties of the emission source in a proper way and provides a simple computational approach for estimating the density and magnetic strength distribution of the source region of the radio bursts.  That could be useful in several astronomical contexts.

*Based on the recent article: Alielden, K. (2022). Characteristics of stripes-pattern radio-emission sources. Monthly Notices of the Royal Astronomical Society, 514(2), 2135-2144. DOI:10.1093/mnras/stac1384

Author address: Department of Physics, Aberystwyth University, Penglais, Aberystwyth, Ceredigion SY23 3BZ, UK