Electromagnetic emissions at the third harmonic of the plasma frequency $\omega _{p}$ have been reported during the occurrence of type II and type III solar radio bursts (e.g. Zlotnik 1978, Zlotnik et al. 1998, Cairns; 1986), even if rarely and sometimes controversially. Recently the Wind spacecraft detected several events exhibiting third harmonic emissions in interplanetary type III bursts observed locally near 1 AU (Reiner and MacDowald; 2019). For the first time, the impact of plasma density fluctuations on the wave coalescence mechanisms responsible for the generation of $\mathcal{H}_{3}$ and $\mathcal{H}_{4}$ electromagnetic harmonics at $3\omega_p$ and $4\omega_p$, is shown.
In a two-dimensional simulation box, an electron beam with velocity $v_{b}=0.25c$ and density $n_{b}/n_{0}=5×10^{-4}$ ($n_{0}$ is the density of the background ions) propagating along the $x$-axis generates Langmuir wave turbulence in (i) an inhomogeneous plasma typical of type III bursts regions in the solar wind, with background random density fluctuations $\delta n$ of average level $\Delta N=\langle (\delta n/n_{0})^{2}\rangle ^{1/2}\simeq 0.05$ and wavelengths much larger than the Langmuir waves’ ones, and (ii) the same plasma but without initially applied density fluctuations. Details on physical and numerical parameters were given in recent papers (Krafft and Savoini, 2021, Krafft and Savoini, 2022).
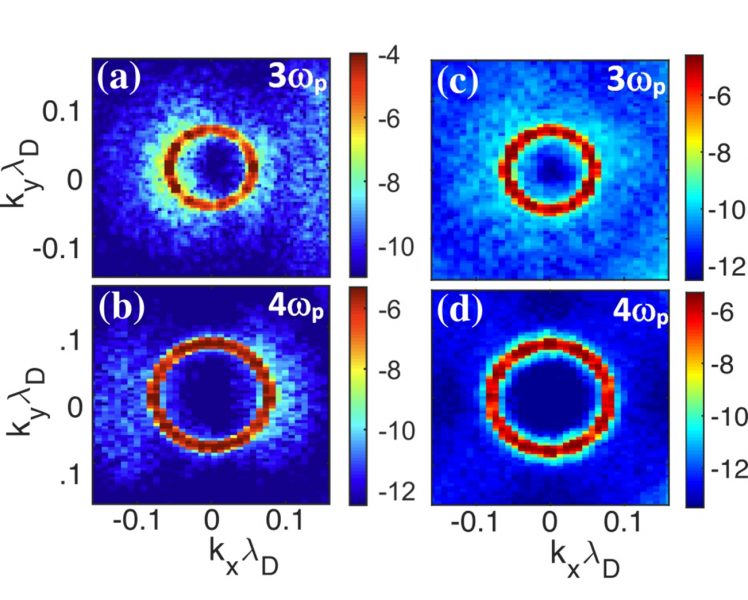
Figure 1: Wave spectra in the plane $(k_{x},k_{y})$, in logarithmic scales. (Left) Homogeneous plasma ($\Delta N=0$) at asymptotic time $\omega _{p}t=8760$: (a) $|B_{zk}|^{2}$ at $\omega _{k}\simeq 3\omega _{p}$: wave $\mathcal{H}_{3}$. (b) $|B_{zk}|^{2}$ at $\omega _{k}\simeq 4\omega _{p}$: wave $\mathcal{H}_{4}$. (Right) Inhomogeneous plasma ($\Delta N=0.05$) at asymptotic time $\omega _{p}t=7150$: (c) $|B_{zk}|^{2}$ at $\omega _{k}\simeq 3\omega _{p}$: wave $\mathcal{H}_{3}$. (d) $|B_{zk}|^{2}$ at $\omega _{k}\simeq 4\omega _{p}$: wave $\mathcal{H}_{4}$. All variables are normalized.
Fig. 1 shows, at asymptotic times, the spectral electromagnetic energy densities $|B_{zk}|^{2}$ in the plane $(k_{x},k_{y})$, at $\omega _{k}\simeq n\omega _{p}$ ($n=3,4$), for $\Delta N=0$ (left column) and $\Delta N=0.05$ (right column). The circular rings representing the electromagnetic waves $\mathcal{H}_{3}$ and $\mathcal{H}_{4}$ can be clearly observed. Whereas for the homogeneous plasma case these distributions exhibit some angular dependence, they show scattering, broadening and isotropization for the inhomogeneous case, due to Langmuir waves’ transformations on density fluctuations, as well as a noticeable reduction of the energy density of waves compared to $\Delta N=0$.
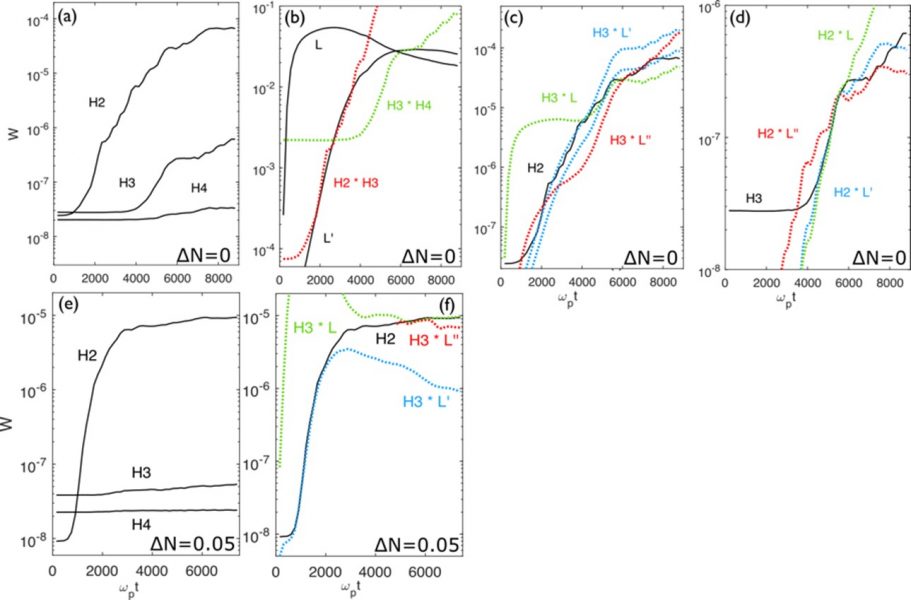
Figure 2. Time variations of wave energies (black curves) and products between them (color curves), in logarithmic scale. (a) $\Delta N=0$: Time variations of $W_{\mathcal{H}_{2}}, $ $W_{\mathcal{H}_{3}}$ and $W_{\mathcal{H}_{4}}$ (black). (b) $\Delta N=0$ : Time variations of $ W_{\mathcal{L}}$ and $W_{\mathcal{L}^{\prime }}$ (black), $W_{\mathcal{H} _{3}}W_{\mathcal{H}_{4}},$ and $W_{\mathcal{H}_{2}}W_{\mathcal{H}_{3}}$, labeled by $H_{3}\ast H_{4}$ (green), $H_{2}\ast H_{3}$ (red). (c) $\Delta N=0$ : Time variations of $W_{\mathcal{H}_{2}}$ (black), as well as $W_{\mathcal{H}_{3}}W_{\mathcal{L}},$ $W_{\mathcal{H}_{3}}W_{\mathcal{L}^{\prime}}$ and $ W_{\mathcal{H}_{3}}W_{\mathcal{L}^{\prime \prime }}$, labeled by $H_{3}\ast L$ (green), $H_{3}\ast L^{\prime }$ (blue), and $H_{3}\ast L^{\prime \prime }$ (red); the blue curve is duplicated (i.e. multiplied by another coupling factor) to show the relation $W_{ \mathcal{H}_{2}}\propto W_{\mathcal{H}_{3}}W_{\mathcal{L}^{\prime }}$ occurring at different times. (d) $\Delta N=0$ : Time variations of $W_{\mathcal{H}_{3}}$ (black), as well as $W_{\mathcal{H}_{2}}W_{\mathcal{L}},$ $W_{\mathcal{H}_{2}}W_{\mathcal{L}^{\prime }}$ and $W_{\mathcal{H}_{2}}W_{\mathcal{L}^{\prime \prime }}$, labeled by $H_{2}\ast L$ (green), $H_{2}\ast L^{\prime }$ (blue), and $H_{2}\ast L^{\prime \prime }$ (red). (e) $\Delta N=0.05$ : Time variations of $W_{\mathcal{H}_{2}},$ $W_{\mathcal{H}_{3}}$ and $W_{\mathcal{H}_{4}}$ (black). (f) $\Delta N=0.05$ : Time variations of $W_{\mathcal{H}_{2}}$ (black), $W_{\mathcal{H}_{3}}W_{\mathcal{L}}$, $W_{\mathcal{H}_{3}}W_{ \mathcal{L}^{\prime }}$ and $W_{\mathcal{H}_{3}}W_{\mathcal{L}^{\prime \prime }}$, labeled by $H_{3}\ast L$ (green), $H_{3}\ast L^{\prime }$ (blue), and $H_{3}\ast L^{\prime \prime }$ (red). Energies are normalized by the initial beam kinetic energy.
Figs.2a and 2e present the time variations of the magnetic energies $W=(1/2)\iint B^{2}(x,y)dxdy$ of the waves $\mathcal{H}_{2},$ $\mathcal{H}_{3}$ and $\mathcal{H}_{4}$ (see also Krafft and Savoini, 2021, Krafft and Savoini, 2022), for $\Delta N=0$ and $\Delta N=0.05$, respectively. The energy ratios $W_{\mathcal{H}_{3}}/W_{\mathcal{H}_{2}}$ and $W_{\mathcal{H}_{4}}/W_{\mathcal{H}_{3}}$ are consistent with radio bursts’ observations. The presence of density fluctuations reduces by less than one order of magnitude the energies carried asymptotically by the electromagnetic harmonics. The efficiency to extract energy from $\mathcal{H}_{2}$ ($\mathcal{H}_{3}$) waves to generate $\mathcal{H}_{3}$ ($\mathcal{H}_{4}$) waves is significantly larger for $\Delta N=0.05$ than for $\Delta N=0$. In the homogeneous plasma, the dominant process generating the harmonic $\mathcal{H}_{3}$ is the coalescence of $\mathcal{H}_{2}$ with a Langmuir wave, $\mathcal{H}_{2}+% \mathcal{L}^{\prime }\longrightarrow \mathcal{H}_{3}$ , where the backscattered wave $\mathcal{L}^{\prime}$ comes from the first cascade of the electrostatic decay $\mathcal{L} \longrightarrow \mathcal{L}^{ \prime }+ \mathcal{S}^{\prime }$, as shown in Fig. 2b where $W_{\mathcal{L}^{\prime }}\propto W_{\mathcal{H}_{2}}W_{\mathcal{H}_{3}}$ and in Figs. 2(c-d) where $W_{\mathcal{H}_{2}}\propto W_{\mathcal{H}_{3}}W_{\mathcal{L}^{\prime }}$ and $W_{\mathcal{H}_{3}}\propto W_{\mathcal{H}_{2}}W_{\mathcal{L}^{\prime }}$ . At later times, the coalescence $\mathcal{H}_{2}+\mathcal{L}^{\prime \prime }\longrightarrow \mathcal{H}_{3}$ occurs with the forward propagating wave $\mathcal{L}^{\prime \prime}$ produced by the second cascade ${\mathcal{L}}^{\prime }\longrightarrow \mathcal{L}^{\prime \prime}+\mathcal{S}^{\prime \prime}$, as $W_{\mathcal{H}_{2}}\propto W_{\mathcal{H}_{3}}W_{\mathcal{L}^{\prime \prime }}$ (Fig. 2c) and $W_{\mathcal{H}_{3}}\propto W_{\mathcal{H}_{2}}W_{\mathcal{L}^{\prime \prime }}$ (Fig. 2d). The same conclusions can be stated for the generation of the harmonic $\mathcal{H}_{4}$ (not shown here). When the plasma contains density fluctuations, Langmuir waves’ energies damp after saturation. Nevertheless, the harmonics $\mathcal{H}_{3}$ and $\mathcal{H}_{4}$ can be generated by wave coalescence in spite of the inhomogeneities modifying randomly the waves’ resonance conditions by energy transport in k-space. The dominant processes are the same as for the homogeneous plasma, i.e. the coalescence of harmonics $\mathcal{H}_{2}$ ($\mathcal{H}_{3}$) with a Langmuir wave generating $\mathcal{H}_{3}$ ($\mathcal{H}_{4}$) (see also Fig. 2f where $W_{\mathcal{H}_{2 }}\propto W_{\mathcal{L}^{\prime }}W_{\mathcal{H}_{3}}$).
Based on a recent paper by C. Krafft and P. Savoini,”Third and Fourth Harmonics of Electromagnetic Emissions by a Weak Beam in a Solar Wind Plasma with Random Density Fluctuations“, ApJL 934 L28 (2022) doi: 10.3847/2041-8213/ac7f28
References
Cairns, I. H. 1986, J. Geophys. Res., 91, 2975, doi: 10.1029/JA091iA03p0297568
Krafft, C., & Savoini, P. 2021, ApJL, 917:L23, doi: 10.3847/2041-8213/ac179570
Reiner, M. J., & MacDowall, R. J. 2019, SoPh, 294, 91, doi: 10.1007/s11207-019-1476-973
Zlotnik, E. I. 1978, Soviet Ast., 55, 399
Zlotnik, E. Y., Klassen, A., Klein, K. L., Aurass, H., Mann, G. 1998, A&A, 331, 1087.
