Solar radio radiation is one of the most sensitive emissions during solar eruptions, where type III radio bursts can provide clues for electron acceleration and propagation. Type III radio bursts are widely accepted to result from the plasma emission, which is observationally supported by the presence of Langmuir waves, and excited electromagnetic waves at fundamental and harmonic frequencies from the nonlinear wave coupling (Ginzburg & Zhelezniakov 1958). Such a mechanism has been further developed based on analytical and numerical studies (Yoon 1997). However, it was sometimes argued that this mechanism might not work efficiently when the plasma is more magnetized. Besides, the third or even higher harmonic emissions were observed in some events, and it is not sure whether the plasma emission mechanism can explain these features or not.
Particle-in-cell (PIC) simulations provide a powerful approach to study solar radio bursts from the first principle. We performed 2.5D PIC simulations to investigate type III radio bursts when electron beams with different pitch angles are injected into a strongly magnetized plasma (plasma beta is much smaller than 1).
Simulation results
Figure 1 shows the dispersion diagrams of the electrostatic field Ex (left panels) when the pitch angle of the electron beam is \(\theta=0^{\circ}\),\(\theta=30^{\circ}\), and \(\theta=80^{\circ}\). The black lines represent the electron beam mode. The blue curves indicate the dispersion relation of the fundamental Langmuir waves. The black dashed curves indicate the dispersion relation of the harmonic Langmuir waves. It clearly illustrates that the Langmuir waves at fundamental (L) and harmonic frequencies (2L, 3L, …) are excited by the electron beam – plasma interaction, and the backward Langmuir waves (\(L’\), \(L^{\prime \prime}\), and \(L^{\prime \prime \prime}\)) are, for the first time, found to be generated up to the third harmonic frequencies in the case of the pitch angle \(\theta=80^{\circ}\).

Figure 1. Dispersion diagrams of the electrostatic field Ex (left panels) and the electromagnetic field Ez (right panels) in the cases of the following pitch angles (from top to bottom): \(\theta=0^{\circ}\), \(\theta=30^{\circ}\), and \(\theta=80^{\circ}\).
To understand how these wave modes are produced, we compare in Figure 2 the energy distributions of the third harmonic Langmuir modes to the density fluctuations along the x-direction, in the case of pitch angle of \(\theta=80^{\circ}\). We find both density bumps and cavities, and the density cavities generally correspond to the maxima of wave energy (left panel) and the anti-correlation coefficient is derived to be ~0.52 (right panel). This indicates that the reflecting and scattering of the Langmuir wave packets by the density fluctuations probably plays a key role in generating harmonic Langmuir modes and exciting electromagnetic modes.
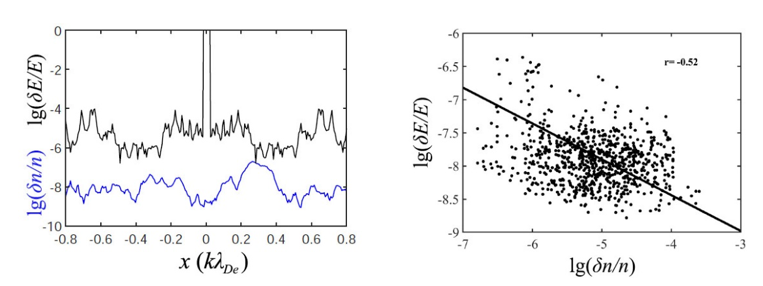
Figure 2. Spatial distributions of the third harmonic Langmuir wave energy and the density fluctuations (left panel) and their anti-correlation (right panel) in the case of pitch angle being \(\theta=80^{\circ}\).
The right panels of Figure 1 display the dispersion diagrams of the electromagnetic field Ez. The solid and dashed curves indicate the theoretical linear fundamental and nonlinear second harmonic electromagnetic dispersion relations. Based on the above results, the radiation processes of the harmonic electromagnetic emission can be explicated as follows. The decay of the Langmuir wave produces backward Langmuir wave and fundamental electromagnetic wave, \(L \rightarrow L’ + F\), and then the coalescence of forward and backward Langmuir waves produces the second harmonic electromagnetic emission, i.e., \(L+L’ \rightarrow 2H\). For the third harmonic electromagnetic emission, three possible processes might be involved: \(L + 2H \rightarrow 3H\), \(L+2L \rightarrow 3H\), or \(L+L’+L^{\prime \prime} \rightarrow 3H\) in the cases of the pitch angle \(\theta=30^{\circ}\) and \(\theta=80^{\circ}\). In order to confirm which process is dominate in our simulations, we conducted the bi-spectral analysis, which can provide potential clues of nonlinear wave coupling. The results reveal the processes of nonlinear wave coupling, \(f_{pe}+f_{pe}\rightarrow 2f_{pe}\), indicating that the second harmonic electromagnetic emission probably corresponds to the coupling of forward and backward Langmuir waves. The higher harmonics may arise from wave coupling as well, that is, \(f_{pe}+2f_{pe}\rightarrow 3f_{pe}\) . The analysis of the bi-spectral analysis at different pitch angles show that the fundamental and harmonic waves are primary, and the other harmonics are all produced by their coalescence. It is therefore clear that the electron beam-driven Langmuir waves act as a kind of “pump” to generate electromagnetic waves via the mode conversion and the nonlinear wave coupling. There is another possibility that cannot be completely ruled out, i.e., the coalescence of electrostatic waves for the third harmonic electromagnetic emission, \(L+L’+L^{\prime \prime} \rightarrow 3H\), especially for the cases of large electron pitch angles.
Summary
Our numerical results indicate the following possible radiation processes of the radio emission: (1) The fundamental electromagnetic emission results from the scattering of Langmuir wave and thermal ions, namely, \(L+i \rightarrow F\), due to the fact that hot plasma was adopted in the simulations. Another possible explanation is the decay of Langmuir waves, namely, \(L \rightarrow S+F\) , where S represents the ion acoustic waves. (2) The second harmonic electromagnetic emission is generated first via the decay of Langmuir waves, namely, \(L \rightarrow L’+F\) , and then via the coupling of forward and backward Langmuir waves, namely, \(L+L’ \rightarrow 2H\). (3) The higher harmonic electromagnetic emission probably results from the coupling of Langmuir waves and harmonic electromagnetic waves, namely, \(L+(n-1)H\rightarrow nH\) (Cairns 1999). It is argued that large pitch angles of the electron beam facilitates the density fluctuations, which further enhance the wave coupling, enabling the higher-order harmonic radio emissions.
Based on the recent paper: T. M. Li, C. Li, P. F. Chen and W. J. Ding. Particle-in-cell simulation of plasma emission in solar radio bursts, A&A 653, A169 (2021). DOI: https://doi.org/10.1051/0004-6361/202140973
References:
Cairns, I. H. 1988, J. Geophys. Res., 93, 858
Ginzburg, V. L., & Zhelezniakov, V. V. 1958, Sov. Astron., 2, 653
Yoon, P. H. 1997, Phys. Plasmas, 4, 3863
