Thermal plasma in the solar corona is often characterized by a range of temperatures. This plasma can be described by the differential emission measure (DEM), which is a distribution of the thermal electron density square over temperature. The DEM-based treatment is widely used in application to the optically thin EUV and X-ray emissions. However, there has been no corresponding treatment in the radio domain, where optical depth of emission can be large, and both free-free and gyroresonance thermal emission mechanisms are involved. A framework that accounts for a multi-thermal plasma composition is highly demanded for analyzing and modeling the currently available data, and needed to combine the EUV, X-ray, and radio models.
Another important factor that is often neglected but can affect the free-free radio emission is the contribution of heavy (highly-ionized) ions. Although abundances of heavy elements relative to Hydrogen are relatively small, their contribution to the free-free emission can be significant due to dependence of the emission on Z2 (the charge square). This contribution depends on both the plasma composition (i.e., the element abundances) and the temperature (i.e., the ionization states).
Method
We have extended the “classical” theory of the thermal free-free and gyroresonance radio emission to the case of a multi-temperature plasma; the new theory has been implemented in a freely-available computer code (Kuznetsov et al. 2021). For the free-free emission, the new theory and code include:
- the multi-temperature plasma composition (described by the DEM), which is applied to both optically thin and thick emissions;
- the temperature-dependent ionization of the elements composing the plasma (which includes the dependence on the element abundances), see Figure 1;
- exact values of the Gaunt factor which determine the Coulomb logarithm, see Figure 1;
- contributions of electron collisions with both ions and neutral (hydrogen and helium) atoms;
- effect of the ambient magnetic field.
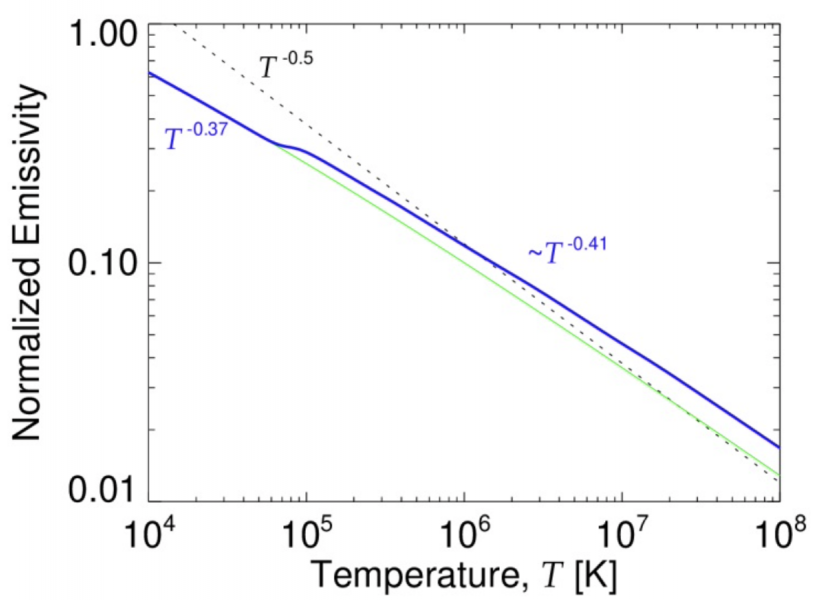
Figure 1 – Dependence of the free-free emissivity at 1 GHz on temperature: green line shows the result for a hydrogen plasma taking into account the exact Gaunt factor, while the blue line also accounts for the temperature-dependent ionization of heavier elements in the solar corona. For comparison, the dotted line shows the T-0.5 dependence.
For the gyroresonance emission mechanism, we have introduced a new measure – the differential density metrics (DDM), which represents a distribution of the thermal electron density over temperature. The new theory and code use this DDM to compute the gyroresonance radio emission from a multi-temperature plasma (the gyroresonance mechanism is insensitive to the element abundances or Gaunt factor).
Similarly to our previous numerical tools for simulating the solar radio emission (Fleishman & Kuznetsov 2010; Fleishman & Kuznetsov 2014), the new computer code computes the radio emission from one or more lines-of-sight by solving the radiation transfer equation. The code also accounts for possible depolarization or polarization reversals when the emission crosses quasi-transverse magnetic field regions.
The new theory is presented in a paper recently published in ApJ (Fleishman et al. 2021). The corresponding computer code is implemented as executable libraries callable from IDL; it is available on GitHub and in the Zenodo repository (Kuznetsov et al. 2021).
Results
Figure 2 shows an example of DDM and DEM distributions obtained from an updated EBTEL code (courtesy of J. Klimchuk; private communication); these distributions will be used below to compute the model emission spectra. The corresponding average plasma temperatures (computed as moments of the distributions) are of about 2.6-2.8 MK, but there are significant amounts of particles with the temperatures considerably above the average values.
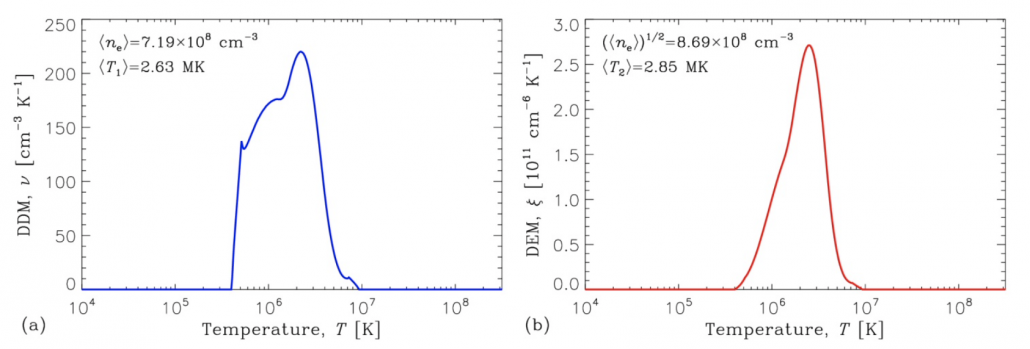Figure 2 – Model DDM and DEM distributions (courtesy of Jim Klimchuk) used in the simulations. The distributions correspond to the plasma heating parameters typical of a solar active region.
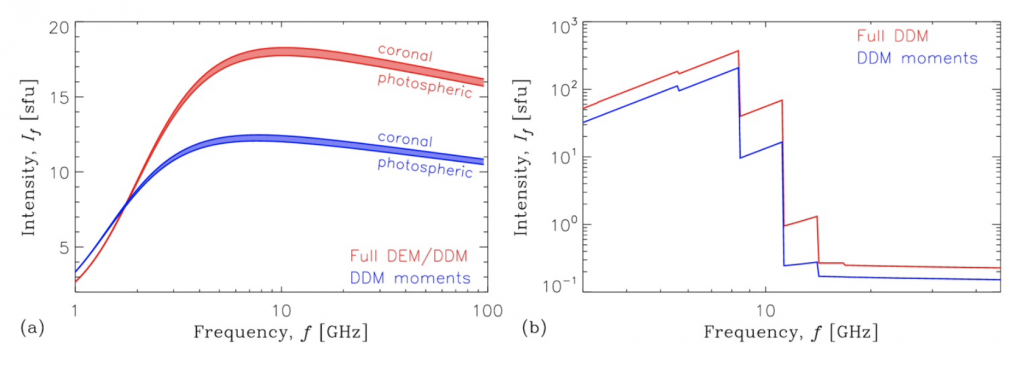Figure 3 – Model radio emission spectra computed using the electron distributions shown in Figure 2. a) Free-free emission (no magnetic field); b) gyroresonance emission (magnetic field varying linearly with height from 1000 to 300 G along the line of sight). The emissions were computed both for the multi-thermal DEM/DDM approach and for an isothermal case corresponding to DDM-averaged temperature and density.
In Figure 3, we compare the free-free and gyroresonance radio emission spectra computed using the new multi-thermal approach and the corresponding (DDM-based) isothermal approximation. For both emission mechanisms, the multi-thermal plasma produces considerably higher emission fluxes, due to the contribution of particles with above-average energies; the difference is up to a factor of ~1.5 for the free-free emission and up to a factor of 2-6 for the gyroresonance emission. For the free-free emission, we have also considered the element abundances typical of either the solar corona or the photosphere/chromosphere; in the corona, due to higher abundances of low-FIP heavy elements (primarily – iron) and hence stronger contribution of highly-ionized ions, the emission intensity is higher by up to 10%.
Additional info: Based on the recent paper by Fleishman, Kuznetsov, & Landi, “Gyroresonance and Free-Free Radio Emissions from Multithermal Multicomponent Plasma”, ApJ, 914, 52 (2021). DOI: 10.3847/1538-4357/abf92c
References
Fleishman, G.D., Kuznetsov, A.A.: 2010, ApJ, 721, 1127
Fleishman, G.D., Kuznetsov, A.A.: 2014, ApJ, 781, 77
Fleishman, G.D., Kuznetsov, A.A., Landi, E.: 2021, ApJ, 914, 52
Kuznetsov, A., Fleishman, G., Landi, E.: 2021, Zenodo:4625572
*Full list of authors: Alexey Kuznetsov, Gregory Fleishman, and Enrico Landi