In the current literature the acceleration of particles during solar flares is attributed to either weak turbulence or to large scale Unstable Current Sheet (UCS). The way UCS drive weak turbulence in a separated volume on the loop top or inside the loops below the UCS was never been presented in detail. During the last thirty years the plasma physics community developed the concept of turbulent reconnection. This concept went unnoticed in the solar physics community, mainly because the possibility that strong turbulence being present in the solar corona, especially during large scale explosions (flares, CMEs), had never been discussed in detail.
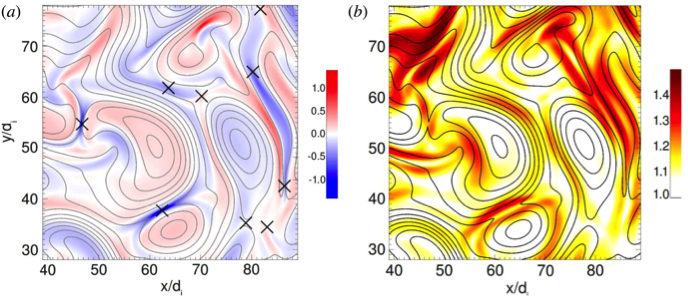Figure 1. (a) Current density (colour) and magnetic field lines, possible reconnection sites are indicated by crosses. (b) The proton temperature (colour). [Servidio, et al., . 2009]
Turbulent reconnection can be generated by different, well known, non-linear MHD processes and structures, which serve as their driver, e.g. the evolution of a spectrum of large amplitude MHD waves, the fragmentation of a current sheet(s), or shock(s), the emerging magnetic flux or the kink instability of unstable loops. Several authors explored the formation of turbulent reconnection in the solar atmosphere, driven by the turbulent convection zone e.g. Parker (1983, 1988), Einaudi and Valli (1994), Galsgaard and Nordlund (1996). All these studies focused on the formation of UCSs; large amplitude magnetic disturbances were thought to be present, yet never analyzed in detail until recently Kontar et al. (2017).
In a recent article, Pisokas, Vlahos and Isliker, in The Astrophysical Journal, (2018) (see also https://arxiv.org/abs/1712.03517), propose that the interaction of electrons and ions with the accelerators is either stochastic when they interact with Alfv\’enic disturbances, as in the model proposed initially by Fermi (1949), or systematic, when they interact with UCSs (Fermi, 1954). The stochastic energization of ions and electrons leads the initial Maxwellian energy distribution to an asymptotic state and the final distribution is a mixture of a hot and an accelerated plasma, with a power law tail with index $\sim 2$. The acceleration time for parameters related with the solar corona is close to a few seconds. In the case of systematic acceleration, when the energy release volume is dominated by UCSs, the particles are mostly accelerated, forming a power law tail with index $\geq 1$ on sub-second time scales, and heating is practically absent.
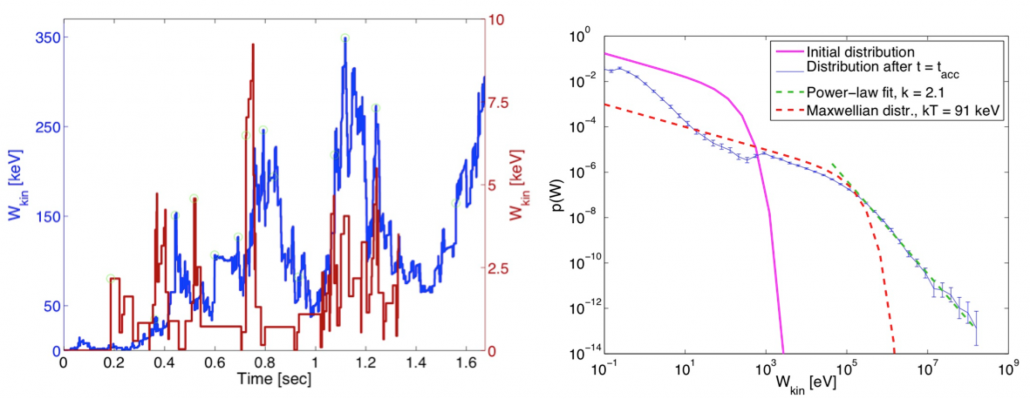
Figure 2. (a) Kinetic energy of typical electrons as a function of time. The stochastic energization is mixed with the systematic energy gain from the UCS, (b) Energy distribution of the electrons interacting with the turbulent reconnecting environment (blue); initial distribution (magenta); Maxwellian fit to the heated low energy region (red dashed), and fit to the power law tail (green dashed). [Pisokas, Vlahos and Isliker, ApJ in press, 2018]
In most laboratory and astrophysical plasmas, the explosive energy release is associated with intense and efficient heating of the bulk of the plasma and with the formation of a power law tail on very fast time scales, see for example the evolution of the photon distribution for solar flares analyzed by Lin (2003). Lin pointed out that in the initial rise of a flare substantial particle acceleration is taking place and in the subsequent impulsive phase a coronal super-hot component appears. A possible explanation for the prompt acceleration and the delayed appearance of the super-hot plasma may be related with the differences in the acceleration times between UCSs and the ASs, as reported above. In summary, the synergy of large scale magnetic disturbances and UCSs in turbulent reconnection can provide the explanation for the appearance of impulsive heating of the super-hot sources and of the non-thermal tails.
Based on a recent article: Pisokas et al., The Astrophysical Journal, 852 64 (2018); DOI: http://doi.org/10.3847/1538-4357/aaa1e0
References
Einaudi,G. and Velli, M., 1994, Space Sci. Rev., 68,97
Fermi, E., 1949, Physical Review, 75,1169
Fermi, E., 1954, ApJ, 119,1
Galsgraad, K. and Nordlund, A., 1996, JGR, 68,97
Kontar, E.P. et al., 2017, PRL, 118, 155101
Lin, R.P., eta al, 2003, ApJL, 595, L69
Parker, E.N., 1983, ApJ, 264, 635