Particle acceleration during solar flares is a highly efficient process, in terms of both the energy (tens of percent of the released magnetic energy can be transferred to the energetic particles) and the particle number (nearly all electrons in the flaring region are accelerated). So-called stochastic acceleration (e.g., Petrosian 2012 for a review) is one of the most popular mechanisms capable of providing these characteristics. In this scenario, the magnetic reconnection produces turbulent outflow that excites an MHD turbulence which then accelerates the particles. The stochastic acceleration mechanism has been studied extensively in many theoretical papers, but until now it has lacked a direct observational confirmation.

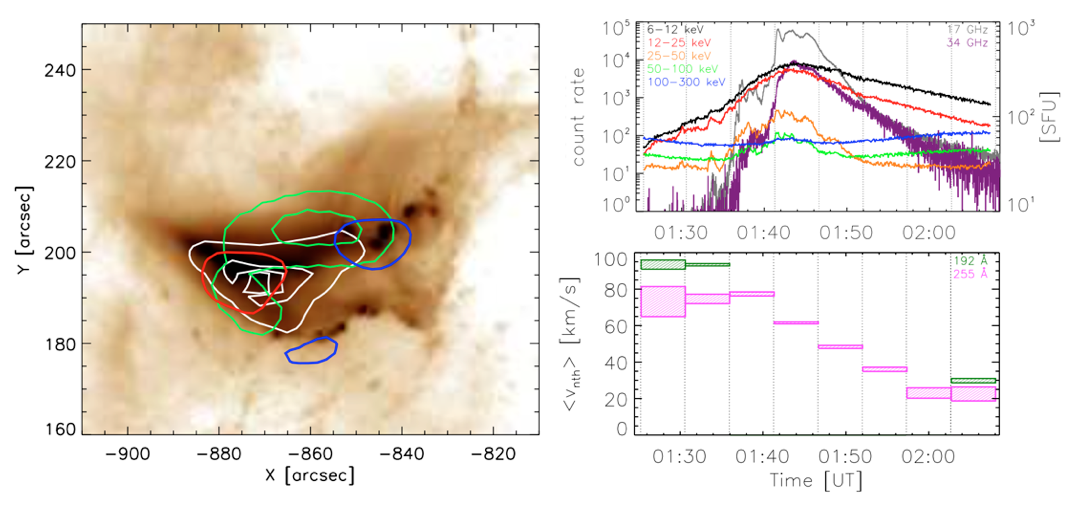
Figure 1. Left: morphology of the flare; background: SDO/AIA 193 Å image, red and blue: 50% RHESSI X-ray contours at 6-15 and 25-50 keV, white: 30% and 75% Hinode/EIS 255 Å contours, green: 30% and 75% Nobeyama Radioheliograph 34 GHz contours. Right top: RHESSI X-ray and Nobeyama Radiopolarimeters light curves. Right bottom: temporal evolution of the nonthermal broadening velocity (from Hinode/EIS) averaged over the coronal X-ray source area.

Observations

We investigated a moderately large (X1.2) and relatively short flare that occurred on May 15, 2013 near the solar limb. This flare was observed in a wide range of wavelengths: from radio to hard X-rays. By using the microwave and hard X-ray images (of the Nobeyama Radioheliograph and RHESSI, respectively), we localized the electron acceleration site (Fig. 1). The microwave and hard X-ray spectral data (of the Nobeyama Radiopolarimeters and RHESSI) allowed us to estimate the magnetic energy stored in the flaring region (~10³¹ erg), the total energy of thermal electrons (up to 10³⁰ erg) and the energy flux of nonthermal electrons (up to ~10²⁸ erg/s), and to reconstruct their temporal evolution (see Fig. 2).

The key part of the study was using the unique cotemporaneous observations from the Hinode EUV Imaging Spectrometer, which provides spatially resolved EUV spectra. Turbulent plasma motions result in nonthermal Doppler broadening of EUV spectral lines (Harra et al. 2013). By analyzing the broadening of the Fe XXIV 255 Å and 192 Å lines, we determined the characteristics of the plasma turbulence, including its amplitude and spatial location. Notably, the location coincided with the acceleration region of the flare. Measurements of the turbulent velocities (up to ~100 km/s) allowed us to estimate the total kinetic energy of the turbulence (up to ~10²⁸ erg) and to plot its temporal evolution (Fig. 2). We detected a good correlation between the kinetic energy of the turbulent plasma and the electron acceleration rate, and the turbulence reached a significant level just before the acceleration rate peak.

It is found (Kontar et al, 2017) that the turbulent kinetic energy comprises only a small part of the total flare energy budget (~0.5-1%). Nevertheless, provided that its energization and dissipation processes are rapid enough (with the timescales of ~1-10 s), the turbulence can channel the released magnetic energy to the hot plasma and energetic particles. For example, Alfvénic MHD turbulence (Goldreich & Sridhar 1995) involves timescales that are consistent with those required. The dissipation of anisotropic Alfvén MHD turbulence occurs on a timescale $L_\perp/\langle v_{nth} \rangle$, where $L_\perp$ is the characteristic scale associated with variations $\delta B$ perpendicular to the guiding magnetic field. The ‘side-on’ geometry of this particular flare on the sky suggests that the observed line-of-sight velocity fluctuations $\langle v_{nth}\rangle$ correspond to motions perpendicular to the guiding field. And although $L_\perp$ is not directly observable, the dissipation timescale can nevertheless be estimated as follows. The energy density associated with a turbulence-perturbed magnetic field $\delta B$ is $U_B \simeq (\delta B)^2/8 \pi$. Equating this to the turbulent energy content $K = (1/2) n \, m \, \langle v_{nth}^2\rangle$, we obtain $\langle v_{nth}^2\rangle \simeq (\delta B)^2/4 \pi n \, m$. Since the Alfv\’en speed $V_A = \sqrt{B^2/4 \pi n \, m}$, it follows that $\langle v_{nth}\rangle/V_A\simeq \delta B/B \simeq L_\perp/L_\parallel$, where $L_\parallel$ is the longitudinal extent of the turbulence region. Thus the dissipation timescale $L_\perp/\langle v_{nth} \rangle$ is approximately the same as the Alfven crossing time $L_\parallel/V_A$, a quantity that is readily ascertainable from observations. Using the  values found in the observations, the dissipation of turbulent energy occurs on a time scale $\sim 1-10$ seconds, a value consistent both with the inferred value of $K/P$ (Figure 2).

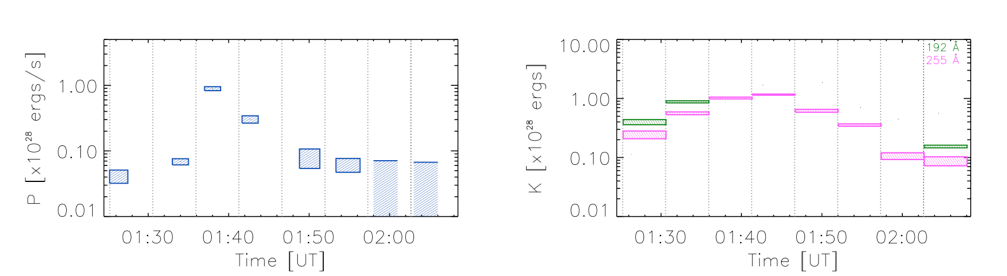
Figure 2. Flare energetics vs. time. Left: total power P (energy flux) in the nonthermal electrons above 30 keV. Right: total turbulent kinetic energy K. The ratio K/P gives dissipation times of 1‑10 s.

Conclusions

The new multiwavelength observations provide persuasive evidence that plasma turbulence plays a key role in the energy transfer in solar flares, thus directly supporting the stochastic acceleration model. The energy dissipation rate and the power in accelerated nonthermal particles observed in the flare are consistent with the dissipation of anisotropic Alfvén MHD turbulence. The observations could be used to test various acceleration models.

*Full list of authors: E.P. Kontar, J.E. Perez, L.K. Harra, A.A. Kuznetsov, A.G. Emslie, N.L.S. Jeffrey, N.H. Bian, & B.R. Dennis

Based on a recently published article:

Kontar, E., Perez, J., Harra, L., Kuznetsov, A., Emslie, A., Jeffrey, N., Bian, N., & Dennis, B. (2017). Turbulent Kinetic Energy in the Energy Balance of a Solar Flare Physical Review Letters, 118 (15) DOI: 10.1103/PhysRevLett.118.155101

References:

Goldreich, P. and Sridhar, S., Astrophysical Journal, 438, p. 763, 1995

Petrosian, V., Space Science Reviews, 173, p. 535, 2012.

Harra, L. K. et al,  Astrophysical Journal, 774, id. 122, 2013.