The extended solar corona and the solar wind is a rich testbed for studying the properties of magnetohydrodynamic (MHD) turbulence. While most solar wind turbulence theories only treat incompressible turbulence, density irregularities are present in the solar wind, and are manifested through fluctuations in the refractive index. Knowledge of density turbulence impacts our understanding of the solar wind significantly, and is important for interpreting a variety of observations. It is linked to our basic understanding of the compressibility of solar wind turbulence. It is also key to infer radio wave scattering leading to depressed quiet Sun brightness temperatures at low radio frequencies, the dissipation of solar wind turbulence, leading to extended solar wind heating, energetic particle propagation through the heliosphere and other interesting problems. The present analysis describes a) the manner in which the amplitude of turbulence ($C_{N}^{2}$) and the modulation index ($\epsilon_N = \delta N/N$) vary with heliocentric distance in the solar wind and b) of the solar cycle dependence of these quantities.
Observations
We have used Crab occultation observations (see Figure 1) made in 2011 and 2013 at the Gauribidanur observatory (Ramesh et al., 2011), together with published data from several earlier observations over the interferometer baselines $60-1000$ meters and frequencies $26-158$ MHz. We have scaled these measured structure functions to a baseline of 1600 meters and a frequency of 80 MHz, which were the parameters corresponding to Crab occultation observations in 2011 and 2013.
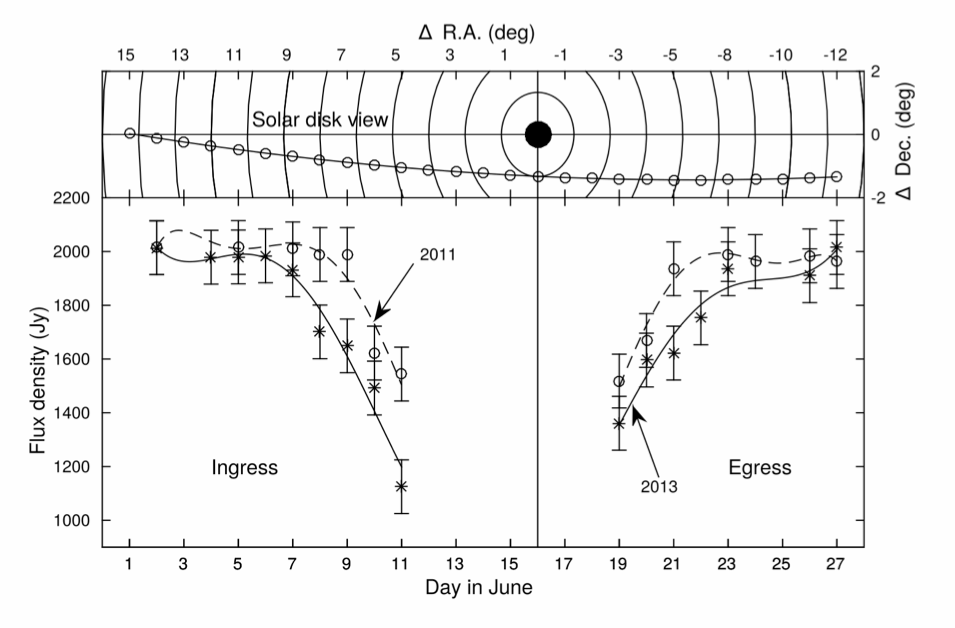
Figure 1: The upper panel shows solar disk view of the Crab nebula occultation. The filled circle indicates the Sun and open circles represent the position of the Crab nebula with respect to the Sun on different dates; $\Delta$ R.A. and $\Delta$ Dec are the offset distances of the Crab nebula from the Sun in right ascension and declination respectively. The closest concentric circle around the Sun has a radius of $5~R_{\odot}$ and the radii of the rest of the circles differ from their adjacent ones by $5~R_{\odot}$. The bottom panel shows the observed flux densities of the Crab nebula on different days during its occultation by the solar corona. The periods before and after June 16th correspond to the ingress and egress, respectively. The plots marked `o’ and `*’ correspond to measurements during June 2011 and June 2013, respectively.
Results and Discussions
We used Crab nebula occultation observations to obtain a comprehensive palette of results concerning the heliocentric dependence of the $C_{N}^{2}$ and $\epsilon_{N}$ in $10 < R < 45 R_{\odot}$. We include the effects of the inner scale using currently prevalent models for it. Since the spatial scales used are small enough to possibly be comparable to the inner/dissipation scale, we use the general structure function (GSF) to model the observed visibilities rather than asymptotic approximations. Since there is evidence for flattening of the spectrum near the inner scale, we quote results for both $\alpha = 11/3$ and 3. We parametrize the heliocentric dependence of the density turbulence amplitude as $C_{N}^{2}(R) = A\,R^{-\gamma}$; the values of $A$ and $\gamma$ from our observations were measured. Figure 2 shows the power law fit to the measured quantities in the year 2013.
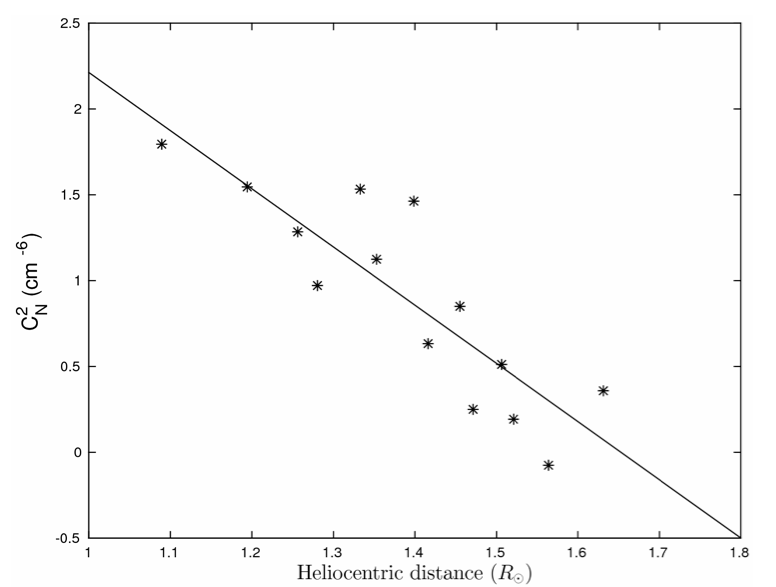
Figure 2: A log-log scatter plot of $C_{N}^{2}$ against heliocentric distance (in $R_{\odot}$) derived from observations in 2013. We use $\alpha=3$ and the inner scale is the proton inertial length. The fit to $C_N^2(R)=A~R^{-\gamma}$ yields $\gamma = 3.4$ and $A = 4 \times 10^{5}~{\rm cm}^{-6}$.
Since we have used data from varying stages of the solar cycle, we investigate the solar cycle dependence of $A$ and $\gamma$; the results for which are summarized in Figure 3 were obtained assuming $\alpha=3$. In the original paper, we also presented the results obtained assuming $\alpha=11/3$. The behavior of $A$ confirms the well known fact that the overall strength of scattering increases with increasing solar activity and vice-versa. Our results for $\gamma$ imply that the scattering amplitude decreases more rapidly with heliocentric distance with increasing solar activity. This is intriguing, and could reflect the increasingly multipolar nature of the large-scale coronal magnetic field near solar maximum, since higher order multipoles decay more rapidly with distance.
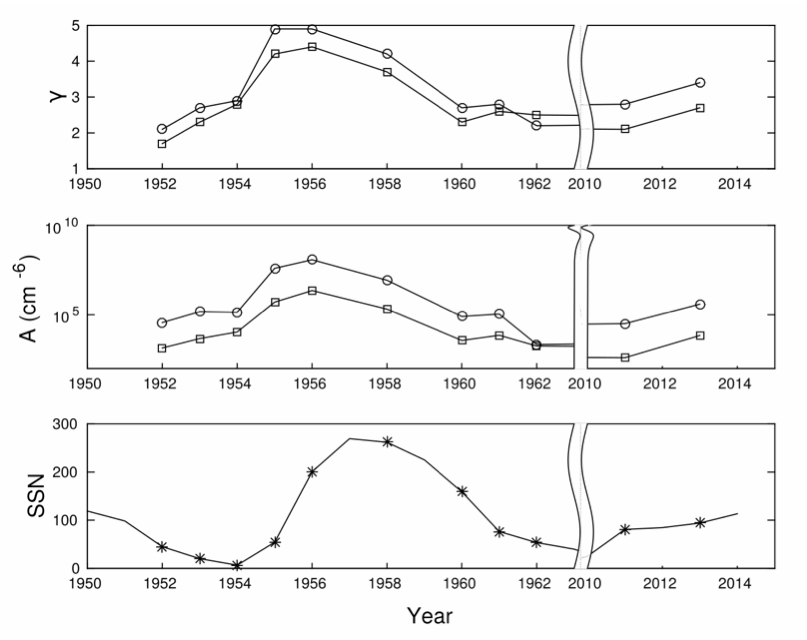
Figure 3: The top panel and middle panel show $\gamma$ and $A~(cm^{-6})$ respectively as a function of time. The `circles’ and `squares’ represent the proton inertial and proton gyroradius inner scale models respectively with $\alpha=3$. For the proton gyroradius model, we use a temperature of $10^5$ K. The solid line in the bottom panel shows the yearly averaged sunspot number and the `*’ represents the year in which the Crab occultation measurements were made. It is evident that both $\gamma$ and $A$ correlate well with the solar cycle.
We also use our knowledge of $C_{N}^{2}$ to obtain the density modulation index. In agreement with the results of Bisoi et al., [2014a] for larger heliocentric distances, we find that $\epsilon_{N}$ depends only weakly on heliocentric distance (see Figure-4). While Bisoi et al., [2014a] found that $\epsilon_{N}$ shows a monotonic decline of around $8 \%$ over solar cycle 23, we find that $\epsilon_{N}$ closely tracks the solar cycle as shown in Figure 5, with a peak-to-peak variation (from 1956 to 1962) of around $72 \%$.
Summary
We report on the amplitude of the density turbulence spectrum ($C_{N}^{2}$) and the density modulation index ($\delta N/N$) in the solar wind between $10$ and $45 R_{\odot}$. These quantities are derived using a GSF that is observationally constrained by occultation observations of the Crab nebula made in 2011 and 2013 and similar observations published earlier. This work yields a comprehensive picture of a) the manner in which $C_{N}^{2}$ and $\delta N/N$ vary with heliocentric distance and b) of the solar cycle dependence of these quantities.
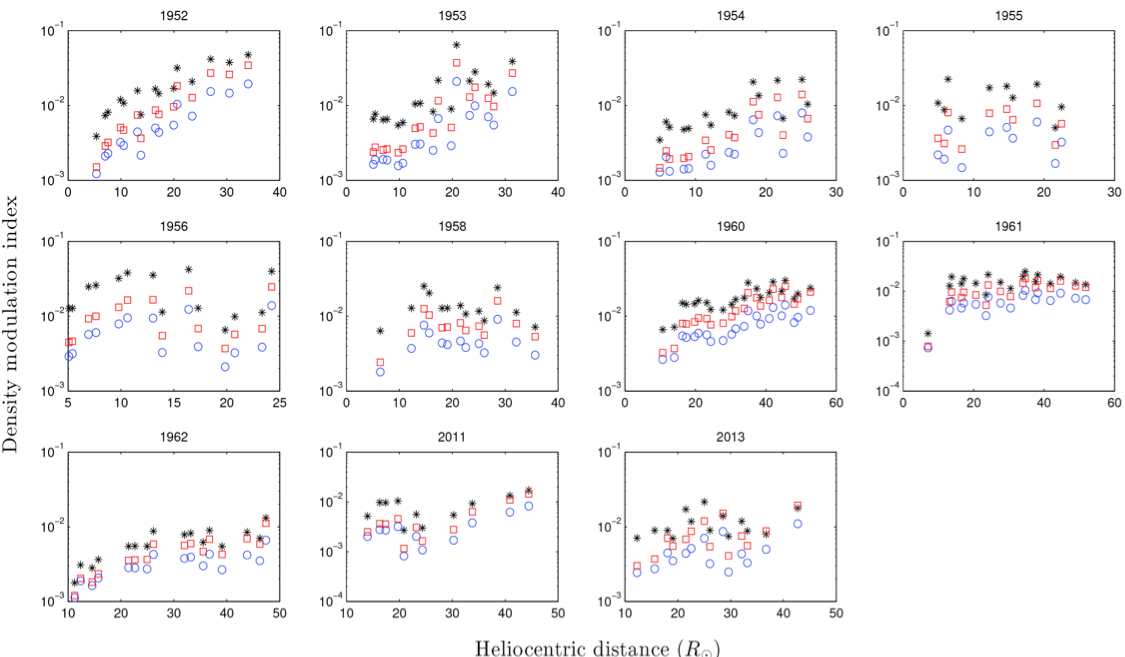
Figure 4: The Figure shows the measured density fluctuation index ($\epsilon_N$) over a heliocentric distance in different years using different inner scale models. The `*’ indicates the proton inertial length model and `circles’ and `squares’ represent the proton gyroradius model with proton temperature $10^5$ and $1.5 \times 10^6$ K respectively.
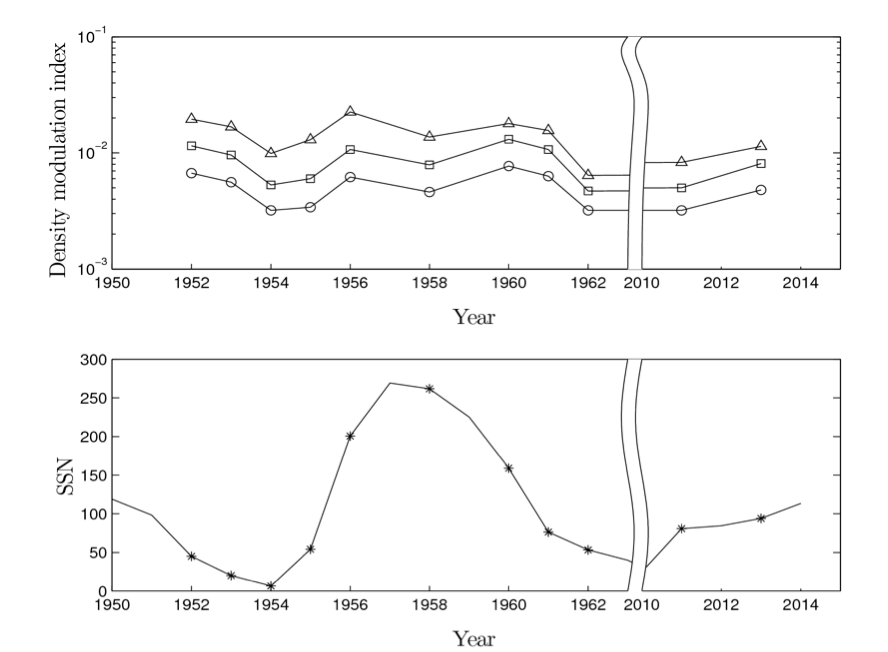
Figure 5: The top panel of the Figure shows variation of the density fluctuations in different years is an evidence of their dependence on solar cycle. The `triangles’ indicate the proton inertial length model and the `circles’ and `squares’ indicate the proton gyroradius model with the proton temperature $10^5$ and $1.5 \times 10^6$ K respectively. In the lower panel, `*’ indicates the average sunspot number on corresponding years.
Additional information
This article is based on the recently published paper:
Sasikumar Raja, K., Ingale, M., Ramesh, R., Subramanian, P., Manoharan, P., & Janardhan, P. (2016). Amplitude of solar wind density turbulence from 10 to 45, Journal of Geophysical Research: Space Physics, 121 (12), 11-11 DOI:10.1002/2016JA023254
References
Bisoi, S. K., et al. (2014), A Study of Density Modulation Index in the Inner Heliospheric Solar Wind during Solar Cycle 23, The Astrophysical Journal, 795, 69.
Ramesh, R. (2011), Low frequency solar radio astronomy at the Indian Institute of Astro-physics (IIA), Bull. Astron. Soc. India Conf. Ser., 2, 55.
*Full list of authors: Sasikumar Raja, Madhusudan Ingale, R. Ramesh, Prasad Subramanian, K. Manoharan, and P. Janardhan
