Langmuir waves that generate type III radio bursts are excited by high-energy electron beams streaming out from the corona through interplanetary space. Despite a smooth temporal distribution of electrons, the Langmuir waves are measured to occur in discrete clumps, commonly attributed to the turbulent nature of the solar wind electron density (e.g. Smith and Sime 1979, Melrose et al 1986). But how do fluctuations in the background plasma shape the distribution of the clumps?
Electron beams near the Earth
To isolate the effect of density fluctuations, we ran nine identical electron beam simulations using our 1D kinetic model except that we varied the intensity of density fluctuations, $\Delta n/n$ from zero to 3%. We set electron beam and background plasma parameters to be comparable to measurements near the Earth, with the mean background electron density constant. Figure 1 shows a snapshot of the electric field intensity from excited Langmuir waves.
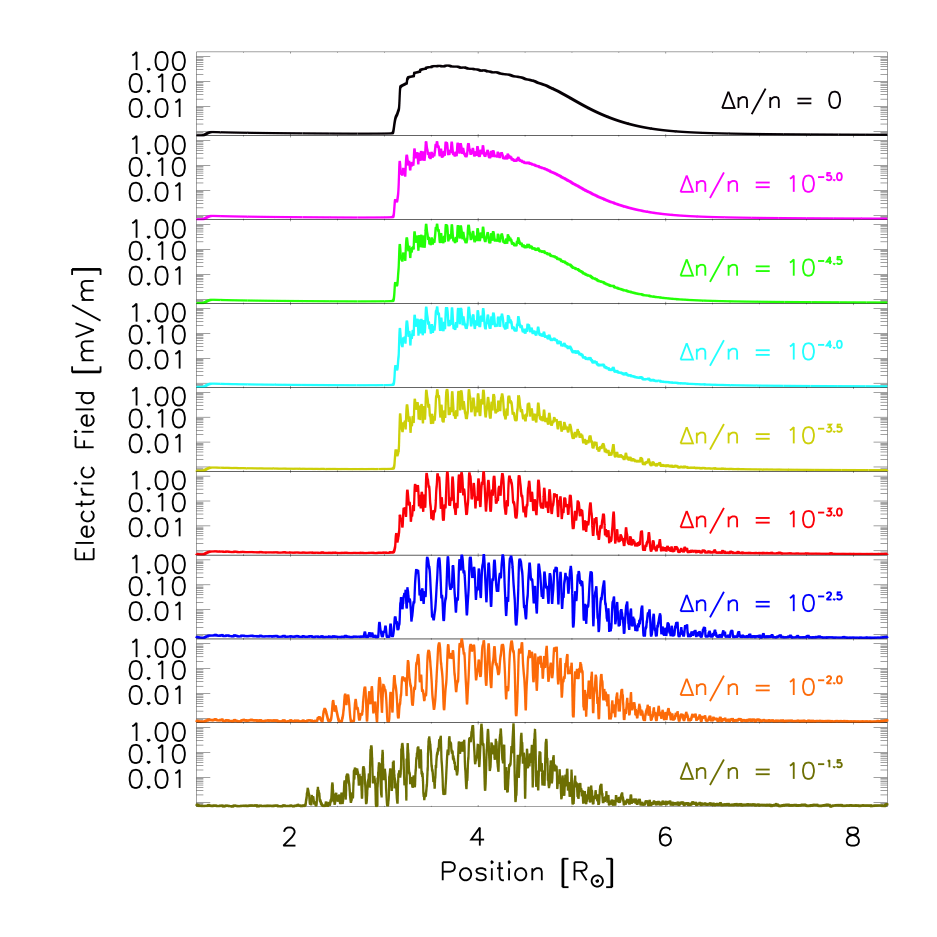
Figure 1: Enhanced electric field generated by a travelling electron beam in plasma with different levels of density fluctuations; zero at the top, increasing to 3% at the bottom.
As the level of density fluctuations in the background plasma was increased, the clumpyness of the Langmuir waves increased. When fluctuations are present, Langmuir waves are refracted off the changing density gradients, clumping in regions of space favourable to Langmuir wave generation. How are these clumps distributed? The resulting probability distribution of the electric field is shown in Figure 2.
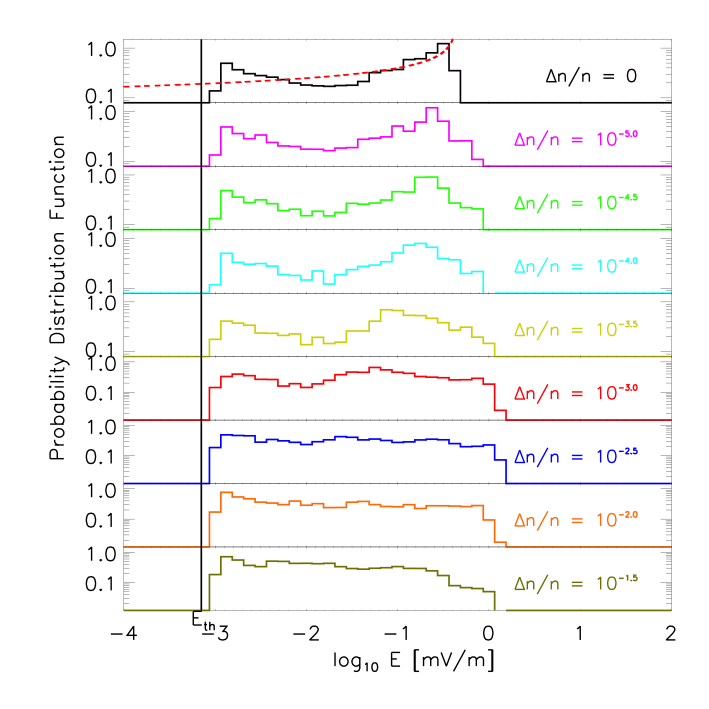
Figure 2: Probability distribution function of the electric field shown in Figure 1. The background thermal level Eth is indicated by the vertical black line
The distribution of the electric field is bimodal. The front of the electron beam, where beam densities are low, generates an electric field distribution that is peaked at the lowest electric fields. The main body of the electron beam produces the highest electric fields, with a distribution that is peaked at the highest electric fields when there are no fluctuations present in the background, predicted from gas-dynamic theory (e.g. Mel’nik et al 1999). When density fluctuations are present, the electric fields become clumped and the corresponding distribution at the highest electric fields spreads out; the variance increases and the mean decreases as the level of fluctuations increases. The change in the mean and variance of the distribution is consistent with the predictions from resonant broadening by density fluctuations from Bian et al 2014.
Electron beams through the Heliosphere
As Solar Orbiter and Solar Probe Plus are going to be flying through the inner heliosphere soon, what is our prediction of how the distribution of the clumps vary close to the Sun? We simulated electron beams injected into the solar corona and propagated through the heliosphere, like Reid and Kontar 2013. This time the mean background electron density gradient was not constant but decreased as a function of distance from the Sun, akin to the solar corona and solar wind plasma. The electron beam and background plasma parameters were comparable to remote sensing measurements. Figure 3 shows the electric field and corresponding distribution for one simulation at different times.
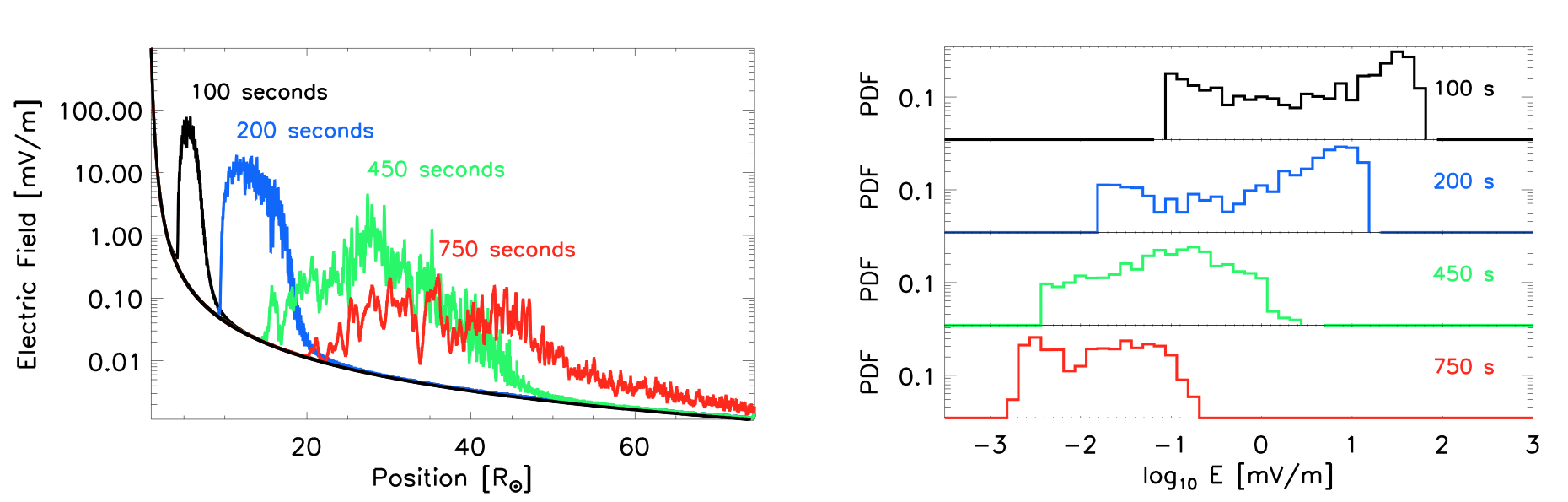
Figure 3: Enhanced electric field generated by an electron beam travelling from the Sun, through the heliosphere at different times. The PDF of the electric field is also shown.
We found similar results that increasing the level of density fluctuations changed the distribution of the electric fields, increasing the variance and decreasing the mean. We also found that the level of density fluctuations played a significant role in determining where the highest level of Langmuir waves above the background was produced. This is inferred from type III radio observations to be at distances corresponding to 1 MHz (Krupar et al 2014).
Conclusions
The clumpy distribution of Langmuir waves is affected by the level of density fluctuations in the background plasma. Simulations show rather complicated forms of the distribution that are dependent upon how the electric fields are sampled. Generally, the higher magnitude of density fluctuations reduces the mean and increase the variance of the distribution in a consistent manor to the predictions from resonance broadening by density fluctuations (see Bian et al, 2014). We also provide a numerical prediction for the in-situ measurements of the upcoming Solar Orbiter and Solar Probe Plus spacecraft.
Additional info
Accepted for publication in Astronomy and Astrophysics. The full work can be accessed here: http://adsabs.harvard.edu/abs/2016arXiv161107901R, corresponding author can be reached at hamish.reid@glasgow.ac.uk. SUPA School of Physics and Astronomy, University of Glasgow (UK).
Based on the recent paper:
Reid, H., & Kontar, E. (2016). Langmuir wave electric fields induced by electron beams in the heliosphere Astronomy & Astrophysics DOI: 10.1051/0004-6361/201629697
References
Bian, N. H., Kontar, E. P., & Ratcliffe, H. 2014, Journal of Geophysical Research (Space Physics), 119, 4239
Krupar, V., Maksimovic, M., Santolik, O., et al. 2014, Sol. Phys., 289, 3121
Mel’Nik, V. N., Lapshin, V., & Kontar, E. 1999, Sol. Phys., 184, 353
Melrose, D. B., Cairns, I. H., & Dulk, G. A. 1986, A&A, 163, 229
Reid, H. A. S. & Kontar, E. P. 2013, Sol. Phys., 285, 217
Smith, D. F. & Sime, D. 1979, ApJ, 233, 998
