It has been known for some time that the size distributions of solar radio bursts and soft X-ray (SXR) flares have steeper power-law slopes (~1.8) than those (~1.2) of solar energetic proton (SEP) events. Hudson (1978) suggested three possibilities for this difference: (1) proton flares are fundamentally different from ordinary flares; (2) proton flares represent the large end of the total energy distribution of ordinary flares; and (3) proton flare characteristics have a threshold behavior. In some sense, each of these conjectures applies, although (1) and (3) are paramount.
Cliver et al. (2012) argued that proton flares are fundamentally different from ordinary flares (hypothesis (1)) because they are eruptive (Kahler et al. 1978). Because of their associated coronal mass ejections (CMEs), proton flares are intrinsically more energetic, satisfying hypothesis (2). Cliver et al. presented evidence for these points by constructing power-law size distributions for (relatively small) samples of large (“gradual”) >10 MeV proton events (58 events), their associated ≥M1 SXR flares (52 events), ≥M1 SXR flares associated with fast (≥1000 km s-1) CMEs (59 events), and ≥M1 soft X-ray flares (540 events). They found that the power-law slopes of distributions of SEP intensity (~1.2) and the peak SXR fluxes of SEP-associated flares (~1.3) were closer to that of the peak SXR fluxes of flares associated with fast CMEs (~1.4) than they were to that of all ≥M1 SXR flares (~2.1). Subsequently, D’Huys et al. (2016) noted that size distribution studies of solar phenomena which use graphical methods (where the power-law exponent is estimated by a linear fit on a log-transformed histogram of the data) ─ as was the case for Cliver et al. (2012) ─ require very large data samples (~103 – 104 events) to provide statistically reliable results. In lieu of such methods, D’Huys et al. advocated use of the more robust maximum likelihood estimator (MLE). Following their suggestion, we revisited the Cliver et al. analysis using the MLE approach.
Analysis and Results
Given a model (in this case, a power law with scaling factor (slope) α), the MLE method obtains an estimate for α by maximizing the likelihood of the data, which is the probability that the data were drawn from that model. The results of applying the MLE to subsamples taken from 136 ~25 MeV SEP events, 113 ≥M1 SEP-associated flares, 159 ≥M1 SXR flares associated with ≥1000 km s-1 CMEs, and 716 ≥M1 SXR flares, are shown in Figure 1. In the figure we see that the pattern for α is similar to that found by Cliver et al. (2012), with the α-values for the peak SXR fluxes of ≥M1 flares associated with SEP events (~1.5; panel (b)) and fast CMEs (~1.6; panel (c)) being closer to that for SEP event intensity (~1.3; panel (a)) than to the α-value for the peak SXR fluxes of all ≥M1 SXR flares (~2.1; panel (d)). As shown by D’Huys et al. (2016), a sample size of at least ~100 events is required to obtain a reliable result with the MLE method, and this minimum value increases as the slope of the distribution increases. These results for SEP-events, SXR flares, and SEP-associated SXR flares are similar to those obtained graphically by Belov et al. (2007) for a larger data sample.
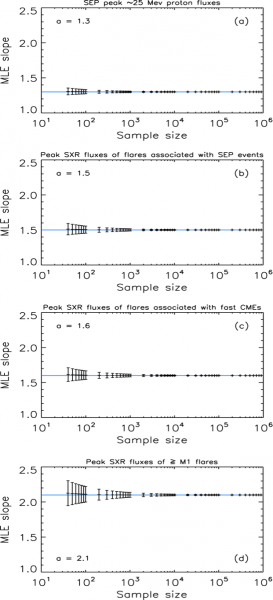
Figure 1. MLE-scaling parameter estimates as a function of sample size for (a) ~25 MeV SEP events, (b) and (c) SXR flares associated with SEP events and ≥1000 km s-1 CMEs, respectively, and (d) ≥M1 SXR flares.
Figure 2 shows that the large SEP events considered here are associated with CMEs with speeds ≳ 400 km s-1, corresponding to the nominal Alfvén speed in the low corona. Thus large SEP events are characteristically accompanied by shockwaves manifested by type II radio bursts in the metric and/or decametric-hectometric (nominally 14 ─ 1 MHz for the Waves experiment on the Wind spacecraft) wavelength range.
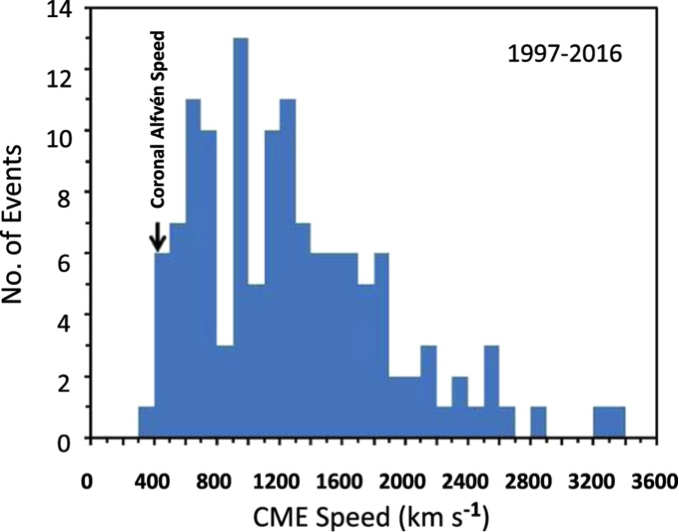Figure 2 Histogram of speeds of CME associated with large ~25 MeV SEP events.
Discussion
Figure 2 shows that Hudson’s (1978) third possible explanation ─ a threshold effect ─ for the difference between the α-values of size distributions of flare electromagnetic emissions and SEP events is also at play. CMEs with speeds > ~400 km s-1 are required to drive the shocks that accelerate protons in large gradual SEP events. Smaller (“impulsive”) SEP events are also commonly associated with CMEs, many with speeds in excess of ~400 km s-1, but for such events the ejected mass is moving along field lines in an X-ray jet magnetic topology (Shimojo & Shibata 2000), whereas movement of magnetoplasma perpendicular to the ambient magnetic field (as in standard loop-like CMEs) is required for shock formation (Vršnak & Cliver 2008).
The key inference or application of the power-law size distributions of flare electromagnetic emissions is the avalanche model of Lu and Hamilton (1991). In that model, based on the self-organized criticality concept, solar flares are viewed as avalanches of small-scale reconnection events. The smaller value of α for SEP size distributions argues for a different physical mechanism for acceleration of the protons that escape into space, one based on fast CMEs and coronal/interplanetary shock waves.
Based on the recent paper: Cliver, E.W., & D’Huys, E.: ApJ, 846, 48, doi: 10.3847/1538-4357/aad043
References
Belov, A., Kurt, V., Mavromichalaki, H., & Gerontidou, M.: 2007, Sol. Phys., 246, 457, doi: 10.1007/s11207-007-9071-x
Cliver, E.W., Ling, A.G., Belov, A., & Yashiro, S.: 2012, ApJ, 756, article id. L29, doi: 10.1088/2041-8205/756/2/L29
D’Huys, E., Berghmans, D., Seaton, D.B., & Poedts, S.: 2016, Sol. Phys., 291, 1561, doi:10.1007/s11207-016-0910-5
Kahler, S.W., Hildner, E., & Van Hollebeke, M.A.I.: 1978, Sol. Phys., 57, 429, doi: 10.1007/BF00160116
Lu, E.T., & Hamilton, R.J.: 1991, ApJ, 380, L89, doi: 10.1086/186180
Shimojo, M., & Shibata, K.: 2000, ApJ, 542, 1100, doi: 10.1086/317024
Vršnak, B., & Cliver, E.W.: 2008, Sol. Phys., 253, 215, doi: 10.1007/s11207-008-9241-5