Electron cyclotron maser emission (ECME) represents a major class of coherent emission mechanism of solar radio bursts. ECME usually occurs in strongly magnetized plasmas with the frequency ratio $\omega_{pe} / \Omega_{ce} < 1$, induced by energetic electrons with $\partial f /\partial v >0$, where $f$ represents the velocity distribution function. In solar active regions, this mechanism has been applied to millisecond spikes which are characterized by high brightness temperatures, short durations, narrow bandwidths, and strong polarizations.
A long-standing problem of ECME accounting for spikes is the escaping difficulty: fundamental emissions ($\omega \sim \Omega_{ce}$) would be absorbed efficiently at the second-harmonic layer where the magnetic field strength is half that at the source (Melrose & Dulk 1982), and thus cannot escape. Emissions at second or higher harmonics ($\omega \sim n\Omega_{ce}$, n=2, 3, …) are more likely to escape. Previous studies using the loss-cone distribution concluded that only fundamental emissions (i.e., $n=1$) can grow via ECME (e.g., Aschwanden 1990).
To investigate the possibilities of harmonic ECME emissions ($n \ge 2$), we conducted fully kinetic electromagnetic 2D3V particle-in-cell (PIC) simulations, in large domains with a huge amount of macro-particles to lower the noise level. We employed horseshoe (Ning et al. 2021a) and loss-cone (Ning et al. 2021b) distributions as the driver of electron cyclotron maser instability (ECMI) to study the wave excitations and the subsequent nonlinear processes.
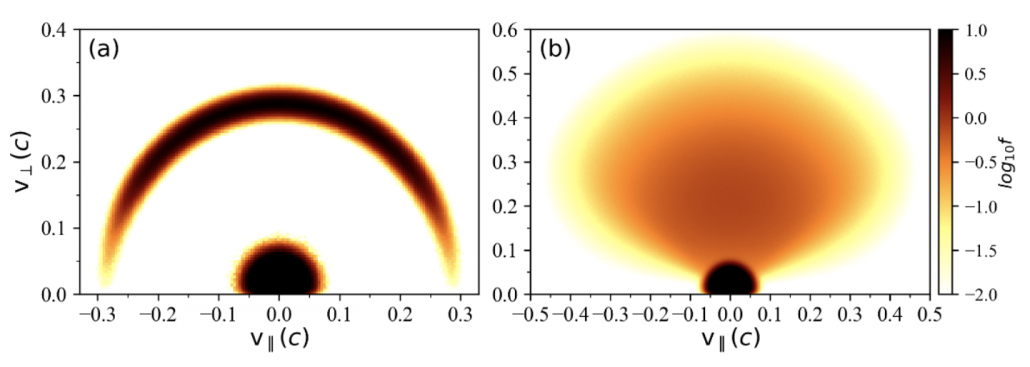Figure 1. Snapshots of the velocity distribution at the beginning of the simulations with horseshoe (a) and loss-cone (b) distributions. The density ratio of energetic electrons to total electrons are set to be 10%.
Horseshoe distribution
According to in situ measurements, auroral kilometric radiations (AKRs) are released by the horseshoe ECME. As an analogy of the AKR, solar spikes have also been associated with energetic electrons of the horseshoe distribution that can form in flare loops with electrons travelling toward lower atmosphere (Melrose & Wheatland 2016).
The horseshoe distribution used to drive the simulation consists of a shell and a double-sided loss-cone distribution (Figure 1(a)). Setting $\omega_{pe} / \Omega_{ce} = 0.1$, we varied the density ratio of energetic electrons to total electrons ($n_e / n_0 $) from 1% to 50%, to simulate the ECME process.
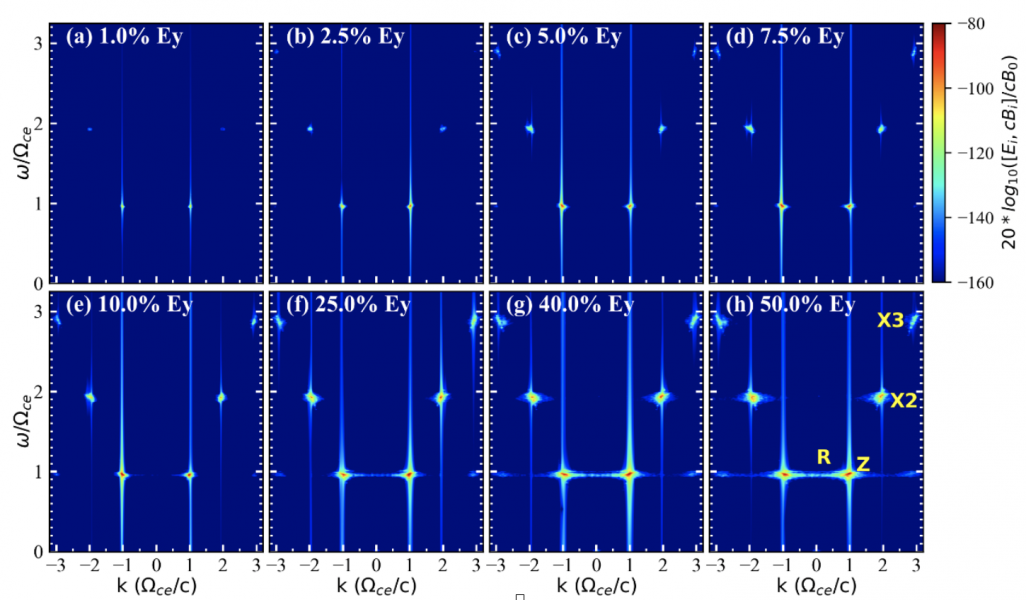
Figure 2. $\omega$-k dispersion diagrams of $E_{y}$ in the perpendicular direction of the simulations with horseshoe distribution with varying $n_{e}/n_{0}$. “Z”, “X2”, “X3”, and “R” stand for the Z mode, second-harmonic X mode, third-harmonic X mode, and the relativistic mode branch.
According to the simulations (Figure 2), the horseshoe distribution can amplify waves in Z and X2 modes (at frequencies of 0.96 and 1.92 $\Omega_{ce}$) efficiently along the perpendicular direction. The X3 mode also grows yet with a lower energy. We note that the amplification of X2 and X3 modes get more efficient with increasing $n_{e} / n_{0}$. With $n_{e} / n_{0}$ ranging from 5% to 50%, we estimated the brightness temperatures of the obtained X2 to be $10^{11}$ K to $10^{15}$ K, consistent with observations of spikes.
Efficient amplification of harmonic emissions provides a solution to the escaping difficulty of the ECME theory. The simultaneous growths of X2 and X3 can explain the multi-harmonic structures observed in solar spikes.
Loss-cone distribution
The loss-cone ECME has been widely investigated by earlier studies, including linear and quasi-linear analyses. However, the non-linear wave-wave interaction has not been well studied. We performed PIC simulation with a long enough duration to study the wave excitations via the loss-cone cyclotron resonance instability, and subsequent wave-wave interaction processes.
We employed a double-sided loss-cone distribution (Figure 1(b)). In the simulation, the value of $\omega_{pe} / \Omega_{ce} = 0.25$, and $n_{e} / n_{0}$ was set to be 10%. The simulation lasts 8000 $\omega_{pe}^{-1}$, representing the longest duration for simulations ever conducted in studies on the same topic.
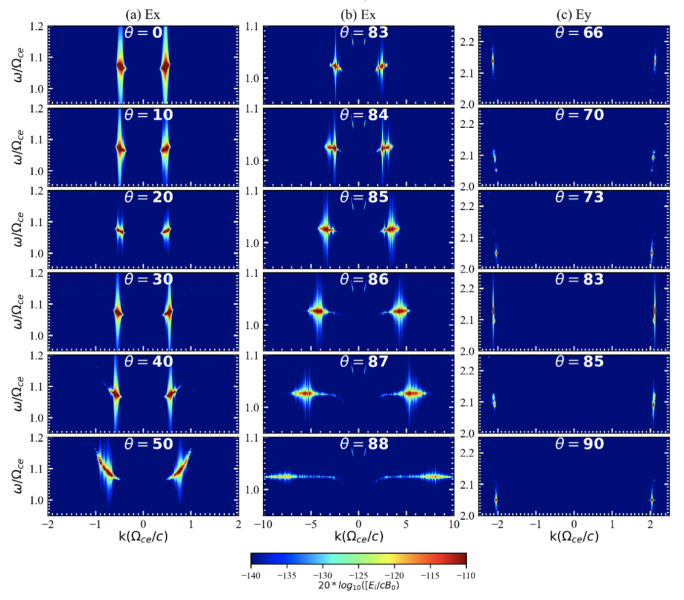
Figure 3. Wave dispersion diagrams of electric fields over 7500-8000 $\omega_{pe}^{-1}$ along different directions. Panels (a), (b), and (c) display the amplified waves in X1, Z, and X2 modes. $\theta$ represent the angle between the directions of wavevector and background magnetic field.
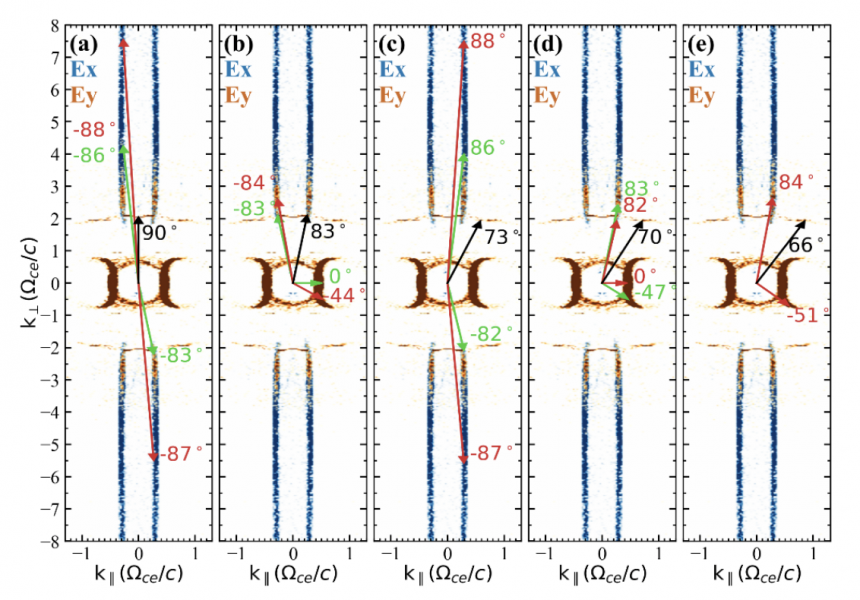
Figure 4. Maximal wave energies in $\vec{k}$ space over 7000–8000 $\omega_{pe}^{-1}$; blue and brown represent results in $E_x$ and $E_y$ components. Possible conditions of wavevectors matching the coalescence condition are overplotted as arrows in the same color. Black arrows represent the wavevector of the target mode to be generated. The values of $\theta$ of each wave vector is marked beside.
Figure 3 shows the dispersion diagrams of the amplified waves in the simulation. We found that the loss-cone distribution could amplify X1 (panel (a); $\omega$~1.06-1.1 $\Omega_{ce}$) and Z (panel (b) $\omega$~1.025 $\Omega_{ce}$) modes via ECMI. As a major result, we obtain strong emissions in X2 along oblique and perpendicular directions at frequencies of 2.05, 2.09, and 2.14 $\Omega_{ce}$, separately (panel (c)).
We suggest that the X2 emissions are produced by nonlinear coalescence processes of Z+X1 and/or Z+Z. This is supported by the following arugments/observations: (1) the matching conditions are well satisfied (Figure 4); (2) X2 emissions are amplified at separate frequencies and discrete angles; (3) X2 starts to grow later than Z and X1. The energy ratio of X2 to Z mode is ~30%, indicating the coalescing process is efficient in energy conversion
For the first time, we obtain efficient excitations of X2 induced by loss-cone electrons via efficient wave-wave coalescing process. Such process represents a novel mechanism of X2 emission in plasmas with a low $\omega_{pe} / \Omega_{ce}$.
Conclusion
We simulated wave excitations by energetic electrons with either horseshoe or loss-cone distribution. We found that the horseshoe distribution could generate X2 and X3 simultaneously via the direct ECME mechanism, while loss-cone distribution could generate X2 through the indirect nonlinear wave-wave coalescence process: the loss-cone ECMI amplify X1 and Z modes first, which then coalesce to generate X2 emissions.
The two studies (Ning et al., 2021a, 2021b) shed new lights on the mechanism of harmonic emissions and the resolution of the long-standing escaping problem of ECME. In our simulations, we obtain efficient excitations of X2, with narrow bandwidth and propagation angles, accounting for high brightness temperatures and strong polarizations of spikes, and explains why only a few percent of the Hard X-ray bursts correlate with spikes.
Based on the recent papers:
Ning, H., Chen, Y., Ni, S.L., Li, C.Y., Zhang, Z.L., Kong, X.L., & Yousefzadeh, M., Harmonic electron-cyclotron maser emissions driven by energetic electrons of the horseshoe distribution with application to solar radio spikes, A&A, 2021a, 651, A118, DOI: https://doi.org/10.1051/0004-6361/202140427
Ning, H., Chen, Y., Ni, S.L., Li, C.Y., Zhang, Z.L., Kong, X.L., & Yousefzadeh, M., Harmonic maser emissions from electrons with the loss-cone distribution in solar active regions, ApJL, 2021b, 920, L40, DOI: https://doi.org/10.3847/2041-8213/ac2cc6
References
Aschwanden, M. J. 1990, A&AS, 85, 1141
Melrose, D. B., & Dulk, G. A. 1982, ApJ, 259, 844
Melrose, D. B., & Wheatland, M. S. 2016, Sol. Phys., 291, 3637
*Full list of Authors: Hao Ning, Yao Chen, Sulan Ni, Chuanyang Li, Zilong Zhang, Xiangliang Kong, and Mehdi Yousefzadeh