Zebra patterns (ZPs) represent a spectral fine structure with equidistant or almost-equidistant stripes of enhanced intensity against a broadband emission background, frequently observed in the dynamic spectra of solar radio bursts such as type IVs. There exist many scenarios for ZPs. The most-accepted one is the model of double plasma resonance (DPR) which, as its name indicates, means simultaneous actions of two kinds of resonance instabilities, i.e., the cyclotron resonance and the upper-hybrid (UH) resonance. DPR is also a result of the electron cyclotron maser instability (ECMI) driven by energetic electrons in plasmas with large ratio of characteristic frequencies ($\omega_{pe} / \Omega_{ce} >> 1$). The DPR process generates plasma waves with sharply-increased growth rates at frequencies close to the upper hybrid (UH) frequency and also an integer times of $\Omega_{ce}$, with $\omega \approx \omega_{UH} \approx s \Omega_{ce}$, where $s$ is an integer. ZPs are suggested to be generated through the conversion process of these plasma waves into escaping radiations, along a large-scale loop structure with gradually-varying $\omega_{pe} / \Omega_{ce}$ (Zheleznyakov & Zlotnik 1975).
Previous studies on DPR are mostly based on linear analysis without considering the generation of escaping radiations due to the non-linear plasma emission process. In a recent study using the fully kinetic electromagnetic particle-in-cell (PIC) simulation, Ni et al. (2020) presented significant plasma emissions at both the fundamental (F) and harmonic (H) branches, via the ECMI process in plasmas with $ \omega_{pe} / \Omega_{ce} = 10$. The process starts from the excitation of various waves, including the UH, Z, and whistler (W) modes, followed by the nonlinear wave–wave coupling process to release the fundamental (F) and harmonic (H) plasma emissions. Ni et al. (2020) suggested that the F emission is generated by the coalescence of almost-counter-propagating Z and W modes, and the H emission is given by the coalescence of almost-counter-propagating electrostatic UH modes.
To investigate the complete generation process of ZPs from the excitation of the DPR instability, the growth of non-escaping wave modes, to the release of escaping radiations, we conduct PIC simulations with values of $\omega_{pe}/\Omega_{ce} $ varying within two adjacent gyro-harmonic bands (9.5–11.5). This also allows us to further examine the occurrence of the above ECMI-plasma emission process through detailed parameter study.
According to the simulations (see Figures 1 and 2), the growths of the UH and Z modes are indeed dominated by the DPR effect, as demonstrated by the variations of their growth rates as well as their intensities with $\omega_{pe}/ \Omega_{ce}$. It was further found that the intensity of the H emission is stronger than that of the F emission by about 2 orders of magnitude. The intensity of the H emission also varies with $\omega_{pe}/\Omega_{ce}$, quasi-periodically, while the F emission is too weak to be significant. This indicates that the ZPs arise from the H emission, rather than the F emission as assumed in many earlier studies. Furthermore, the peak-valley contrast of the total intensity of the H emission (pr ZPs) is about 4, consistent with some observational reports (e.g., Tan et al. 2014). These results are critical to the understanding of the origin of solar ZPs and further diagnostic efforts using radio data with ZPs.
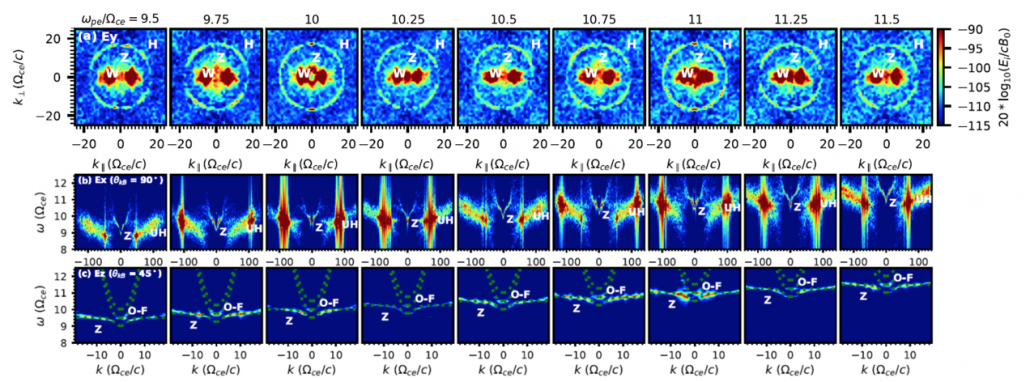 Figure 1 – (a) The wave intensity map in ($k_\parallel, \ k_\perp$) space with $\omega_{pe}/\Omega_{ce} = 9.5 – 11.5$, and (b)–(c) the $\omega-k$ dispersion curves for different modes. “UH” stands for upper hybrid mode, “W” for whistler mode, “Z” for Z mode, “H” for harmonic plasma emission, and “O-F” stands for O mode around the fundamental plasma frequency.
Figure 1 – (a) The wave intensity map in ($k_\parallel, \ k_\perp$) space with $\omega_{pe}/\Omega_{ce} = 9.5 – 11.5$, and (b)–(c) the $\omega-k$ dispersion curves for different modes. “UH” stands for upper hybrid mode, “W” for whistler mode, “Z” for Z mode, “H” for harmonic plasma emission, and “O-F” stands for O mode around the fundamental plasma frequency.
 Figure 2 – (a)–(c) The temporal energy profiles of the five modes normalized to the initial kinetic energy of total electrons ($E_{k0} $). (d) The fitted exponential growth rate of UH, Z, and W modes. (e) The variation of final energy of Z and H modes with $ \omega_{pe} / \Omega_{ce} $. (f) The ZPs generated according to the simulated variation of the H emission, assuming $\Omega_{ce}=14$ MHz and $ \omega_{pe} / \Omega_{ce} =9.5-19.5$. The fluctuations of the simulated ZPs are caused by prescribed fluctuations of plasma densities (or $\Omega_{ce}$).
Figure 2 – (a)–(c) The temporal energy profiles of the five modes normalized to the initial kinetic energy of total electrons ($E_{k0} $). (d) The fitted exponential growth rate of UH, Z, and W modes. (e) The variation of final energy of Z and H modes with $ \omega_{pe} / \Omega_{ce} $. (f) The ZPs generated according to the simulated variation of the H emission, assuming $\Omega_{ce}=14$ MHz and $ \omega_{pe} / \Omega_{ce} =9.5-19.5$. The fluctuations of the simulated ZPs are caused by prescribed fluctuations of plasma densities (or $\Omega_{ce}$).
Based on the recent paper: Li, C., Chen, Y., Ni, S., Tan, B., Ning, H., & Zhang, Z., PIC Simulation of Double Plasma Resonance and Zebra Pattern of Solar Radio Bursts, The Astrophysical Journal Letters, 2021, 909, L5, DOI: https://doi.org/10.3847/2041-8213/abe708
References
Ni, S., Chen, Y., Li, C., et al. 2020, ApJL, 891, L25
Tan, B., Tan, C., Zhang, Y., et al. 2014, ApJ, 790, 151
Zheleznyakov, V. V., & Zlotnik, E. Y. 1975, SoPh, 44, 461
*Full list of Authors: Chuanyang Li, Yao Chen, Sulan Ni, Baolin Tan, Hao Ning, and Zilong Zhang
