Drift-pair bursts are a rare and mysterious type of fine spectral structures in the low-frequency domain of solar radio emission. First identified by Roberts (1958), they appear in the dynamic spectrum as two parallel frequency-drifting bright stripes separated in time; the trailing stripe seems to repeat the morphology of the leading one with a typical delay of ~1–2 s (see, e.g., Figure 1). Recent imaging spectroscopy observations with the LOw-Frequency ARray (LOFAR; van Haarlem et al. 2013) enabled Kuznetsov & Kontar (2019) to study these bursts with an unprecedented spatial, temporal and spectral resolution. In particular, it was found that: a) the emission sources of both components of a drifting pair (at the same frequency) coincide spatially; b) the sources of both components propagate in the same direction along the same trajectory; c) at the decay phases of both components (i.e., shortly after the intensity peaks), the emission sources demonstrate a rapid radial (outward) motion and an increase in size. The latter feature is reminiscent of the source dynamics detected in type IIIb bursts (Kontar et al. 2017) and can be explained naturally by scattering of radio emission during propagation.
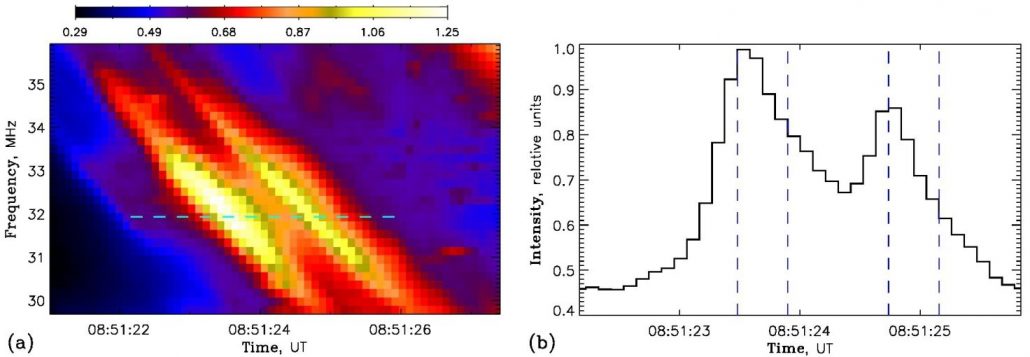
Figure 1. (a) Dynamic spectrum of a typical drift-pair burst recorded with LOFAR on 2017 July 12. (b) Time profile of the radio flux at a single frequency (32 MHz). The figure is adapted from Kuznetsov et al. (2020).
Initially, drift-pair bursts were interpreted by the radio echo effect (Roberts 1958) – reflection of radio waves from lower (denser) layers of the solar atmosphere; however, this model had difficulties with explaining certain observed features, such as the delays between the components, apparent source positions, etc. On the other hand, the first echo models largely ignored the radio-wave scattering; as demonstrated by Kontar et al. (2019), the scattering (especially, anisotropic one) can alter significantly both the apparent radio source positions and light curves. We performed numerical simulations of the radio-wave propagation in a turbulent medium to explore whether the radio echo with anisotropic turbulence can reproduce the observed characteristics of drift-pair bursts.
Method
We employ the 3D Monte Carlo ray-tracing code presented by Kontar et al. (2019). This code simulates the time evolution of the radio-wave packets (“photons”) in the coordinate space and in the space of wavevectors, and accounts for both the refraction/reflection due to large-scale gradual variation of the plasma density and random changes of the propagation direction due to scattering. The anisotropy is characterized by the parameter α, with α < 1 corresponding to preferential scattering in the perpendicular (to the local magnetic field) direction; smaller values of α correspond to higher anisotropy levels. We start the simulations with an isotropic point-like source, the emission frequency slightly above the local plasma frequency (i.e., we consider the fundamental plasma emission), and zero-duration pulse; we then trace ~104 photons until they reach 1 AU sphere and reconstruct the apparent light curve and radio map for an observer at the Earth.
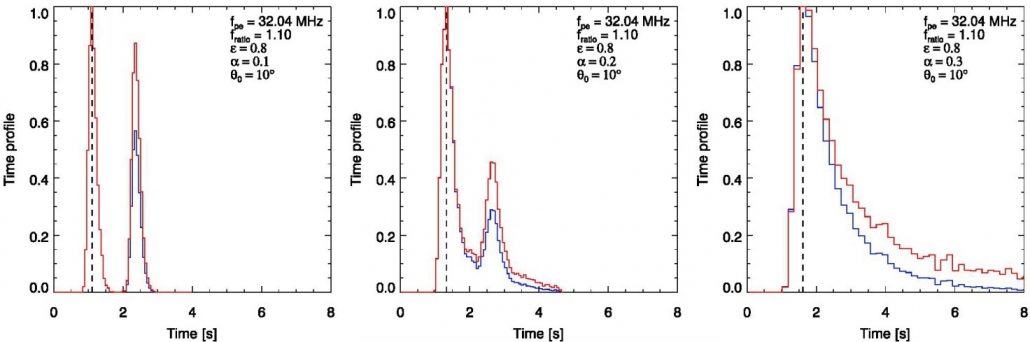
Figure 2. Simulated time profiles of the emission intensity for several levels of plasma fluctuations anisotropy. Blue and red lines represent the signal with and without collisional absorption, respectively. The figure is adapted from Kuznetsov et al. (2020).
Figure 2 demonstrates the simulated light curves for several different turbulence anisotropy levels. For a high anisotropy level of α = 0.1, the light curve has an evident double-peak structure which is very similar to the observed one (Figure 1). Notably, we have found that the apparent sources of both the direct and reflected components coincide spatially, and the simulated source sizes agree with the observed ones, too. For a lower anisotropy level (α = 0.2), the peaks become broader and the second (reflected) component becomes less pronounced. Finally, for even lower anisotropy levels (α ≥ 0.3), the reflected component becomes nearly invisible (i.e., lost in the tail of the direct component).
The amplitude of the second component is determined both by the reflection and scattering processes and by the collisional damping which affects the reflected signal more strongly. Since the collisional damping increases with the frequency, the relative amplitude of the reflected component decreases accordingly; this explains why drift-pair bursts have been observed in a limited range of frequencies (~10–100 MHz) only. Our simulations have demonstrated that the delay between the drift-pair components slowly decreases with frequency, in agreement with observations by Melnik et al. (2005).
Conclusions
We have demonstrated that the anisotropic radio-wave scattering model can quantitatively reproduce the observed features and key properties of the solar drift-pair bursts. Formation of drift-pairs requires: a) anisotropic plasma density fluctuations with typical wavelengths in the perpendicular direction an order of magnitude shorter than in the parallel direction; b) very short emission pulses (much shorter than 1 s); c) relatively low collisional damping, which corresponds to the frequencies below ~100 MHz. The delay between the burst components is sensitive to the emission-to-plasma frequency ratio in the emission source and thus can be used as a diagnostic tool for the plasma emission mechanism.
Additional info: Based on the recent paper by Kuznetsov et al., “Radio Echo in the Turbulent Corona and Simulations of Solar Drift-pair Radio Bursts”, ApJ, 898, 94 (2020). DOI: 10.3847/1538-4357/aba04a
References
Kontar, E.P., Chen, X., Chrysaphi, N., et al.: 2019, ApJ, 884, 122
Kontar, E.P., Yu, S., Kuznetsov, A.A., et al.: 2017, Nat. Commun., 8, 1515
Kuznetsov, A.A., Kontar, E.P.: 2019, A&A, 631, L7
Melnik, V.N., Konovalenko, A.A., Dorovskyy, V.V., et al.: 2005, Solar Phys., 231, 143
Roberts, J.A.: 1958, Aust. J. Phys., 11, 215
van Haarlem, M.P., Wise, M.W., Gunst, A.W., et al.: 2013, A&A, 556, A2
