Estimating the kinematics of Type II radio-burst sources, which are recognized as a shock waves, using electron-density models is inaccurate and restricted. In this article, a blast-expansion technique is used for the first time for estimating the kinematics of a Type II radio-burst source without using electron-density models by studying the density variation along the leading surface of the coronal mass ejections (CMEs) (herein: ejecta) during Type-II radio-burst emission. This technique is valid for analyzing the Type-II radio-burst spectrum in metric and DH frequencies ranges, which was triggered by the ejecta propagation from the corona into interplanetary space.
Observations and results
The flux tube of the ejecta elongates in the latitudinal direction during its propagation. This makes the flux rope deviate from the minimum energy Taylor state. This deviation entails reconnection of the ejecta magnetic-field lines in order to move back towards the minimum energy state. The occurrence of reconnection leads to turbulence (Fermo et al., 2014). In this article, it is proposed that this strong turbulence from the ejecta could propagate without being driven and behaves like a blast wave (hereinafter this phenomenon will be so referred to). This blast wave compresses and drives the medium along the leading surface of the ejecta. The disturbed medium generates plasma emission, the frequency of which depends on the density of the disturbed plasma. Due to the blast wave expansion, that is considered the source of the radio-burst emission, the electron density $n_e$ of the compressed medium decreases by increasing the surface area of the blast wave. It is found that the temporal variation of Type-II radio bursts frequencies $f$ can be described according to the formula
\[ f^2=f_{ei}^2 {\tau^{-\mu}}, \]
where $\mu=0.656$ and $f_{ei}$ is the initial frequency of the emission, that is derived from the Sedov–Taylor blast wave formula. This derived formula was compared with the observed frequencies that recorded by RAD1 and RAD2 receivers of Wind/WAVES experiment as shown in figure 1. The analysis was consistent with the previous work on the MHD condition of the Sedov–Taylor formula (Rogers, 1957) and with statistical studies of the density variation on the surface area of an interplanetary CME (Bothmer et al., 1997).
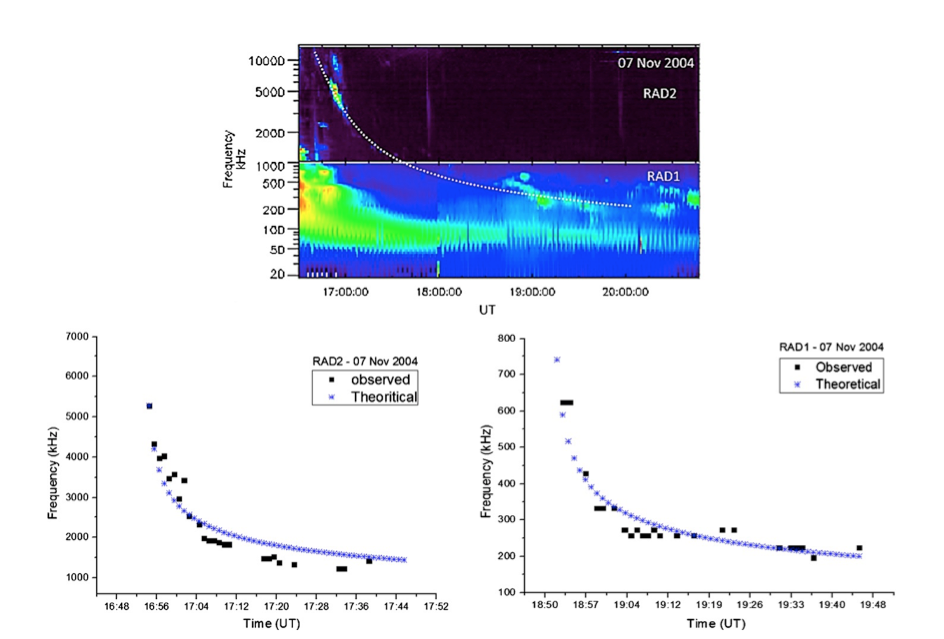Figure 1 – The Type-II radio burst of 7 November 2004. Peak-flux frequency versus time, measured at one-minute time resolution, is shown in the graphs displayed below the radio spectrum as observed by RAD1 and RAD2.
The kinematics of Type II radio-burst source and the temporal variation of its energy are estimated during the Type II radio-burst emission. Furthermore, the splitting between upper-frequency band (UFB) and lower-frequency band (LFB) has been derived to be
\[ \Delta f \approx \frac{1}{2}\ {c_{\mathrm{\lambda}}}\ {f_{\mathrm{e}}} \ (1-{\frac{c_{\mathrm{\lambda}}}{4}}) ,\]
where $c_{\lambda }$ indicates the state of the ejecta. The variable $c_{\lambda }$ describes the relative Alfvén speed $v_{A }$, which depends on the magnetic-field strength and density. The magnetic-field strength of the ejecta is estimated during the Type-II emission by calculating $c_{\lambda }$, estimated from the ratio between the frequency of UFB $f_{U}$ to the frequency of LFB $f_{L}$ .
This blast-expansion technique is valid for different spectra at different regions in the heliosphere. Results of the two case studies show that the energy of the ejecta degraded by $ \approx 14 \%$ of its initial energy at the beginning of metric Type-II radio emission on 16 March 2016, while the energy of the ejecta degraded by $ \approx 86 \%$ and $ \approx 20 \%$ for DH Type-II radio burst as recorded by RAD1 and RAD2 on 7 November 2004, respectively. The splitting [$\Delta f$ ] between UFB and LFB in the metric Type II on 16 March 2016 as estimated using the above equation was 16.56 MHz, whereas the splitting equal 17 MHz from observation. The difference between the values is 0.44 that may arise from to the error in determining the value of frequencies $f_{U}$ or $f_{L}$ in the practical work.
Conclusion
The results suggest that the Type-II radio-burst source is mostly a blast wave. Therefore, the Type II spectra in the RAD1 and RAD2 spectrometers are not continuous; however, they may be generated by the same ejecta with the same mechanism. The analysis shows that the Transversal speed of the blast wave is higher than its radial speed and propagates within a small fraction of $R_{\odot}$ from the point source of the blast wave on the ejecta. The expansion process is one of the mechanisms that degrades the energy of the ejecta during its propagation.
Additional info: Based on the recent paper by Alielden, K., Evolution of Coronal and Interplanetary Shock Waves Inferred from a Radio Burst, Solar Physics, 294, 159 (2019) doi: https://doi.org/10.1007/s11207-019-1493-8
References
Bothmer, V.; Schwenn, R., 1997, Annales Geophysicae, 16, pp.1-24
Rogers, M. H., 1957, Astrophysical Journal, 125, 478
Fermo, Opher, and Drake, 2014, Physical Review Letters, 113, Issue 3, id.031101