We discuss properties of type III bursts that change the sign of their drift rate from negative to positive and vice versa. Moreover, these bursts may change the sign of their drift rates more than once. These particular type III bursts were observed simultaneously by the radio telescopes UTR-2, URAN-2, and NDA in the frequency range 8-41 MHz. The negative drift rates of these bursts are similar to those of previously reported decametre type III bursts and vary from -0.7 MHz/s to -1.7 MHz/s, but their positive drift rates vary in a wider range from 0.44 MHz/s to 6 MHz/s. Unlike inverted U-bursts, the tracks of these type III bursts have C- or inverted C-shapes. Our basic explanation of the positive drift rate of these type III bursts differs from the common assumption that positive drift rates of type III bursts are connected with electron beam propagation toward the Sun. We propose that, even if electron beams move outward from the Sun, they can generate type III bursts with positive drift rates if in some regions of the solar corona the group velocities of type III radio emissions are lower than the velocities of the electron beams.
Observations
Type III bursts with an alternating drift-rate sign were observed by the radio telescopes Ukrainian T-shaped Radio telescope (UTR-2, Kharkov, Ukraine), Ukrainian Radio telescope of the Academy of Sciences (URAN-2, Poltava, Ukraine), and the Nançay Decameter Array, (NDA, Nançay, France) during the summer observation campaign in 2012. At UTR-2 only four sections of the radio telescope were used. The two Ukrainian radio telescopes were equipped with a digital spectral polarimeter of z-modification (DSPz). They enable the recording of radio emission in the continuous frequency band 8-32 MHz/s. The frequency and time resolution of the DSPz used here were 4 kHz and 100 ms. The spectrometer that was used for these observations at NDA had a frequency of 12 kHz and time resolution of 37 ms.
We discuss in the paper (Melnik et al., 2015) three type III bursts with changing frequency drift-rate signs, which were observed on June 3, 2012, August 25, 2012 and August 26, 2012. The dynamic spectrum of one of them, namely the burst registered on August 25, is shown in Figure 1. The drift rate of its forefront was -3.6 MHz/s and 0.95 MHz/s in the frequency ranges 18-32 MHz and 11-18 MHz correspondingly. In the frequency band 21-33 MHz the drift rate of its peak changed sign several times (Figure 1b) with an average negative drift rate of about -1.7 MHz/s. At lower frequencies the drift rate also changed sign several times, but now the average drift rate is positive 1.2 MHz/s. This type III burst together with the preceding one resembles an inverted U-burst (Figure 1a). However, we consider this situation to be accidental because all observed decameter U-bursts have a descending part that is essentially fainter than the ascending one. Normal U-bursts have descending parts with positive drift rates. This means that the electron beam responsible for the descending part propagates toward the Sun. The discussed burst changes the drift-rate sign. Clearly, this needs to be explained even if this burst is considered as the descending part of a U-burst.

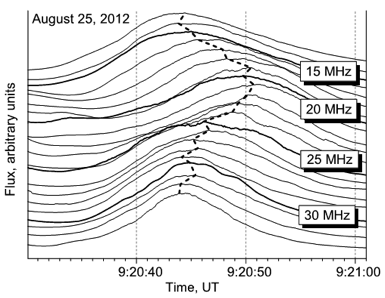
Figure 1. a) Dynamic spectrum of the type III burst with changing drift-rate sign on August 25, 2012 at 09:20:44; b) The time profiles of this type III burst at different frequencies.
Discussion
In our opinion, a possible explanation for a change of drift rate might be the propagation of the radio emission that is generated by fast electrons in a coronal plasma. The frequency drift-rate of a type III burst between frequencies \({f_1}\) and \({f_2}\) is equal to the ratio of frequency difference, \({f_1} – {f_2}\), to the difference of radio emission arrival times at Earth, \({t_1} – {t_2}\) (Figure 2). As was shown by Melnik et al. (2008), this time difference \({t_1} – {t_2}\) is mainly given by the times needed for the electron beam and the electromagnetic wave to travel between the heights \({r_1}\) and \({r_2}\), at which the emissions at frequencies \({f_1} = f({r_1})\) and \({f_2} = f({r_2})\) were generated. Because the group velocity of the fundamental radio emission where it is generated may be much lower than the speed of light, the time difference can be both positive and negative, depending on electron beam velocity and the group velocity, and this defines the drift-rate sign. Following Melnik et al. (2008), a source moving with a constant velocity \({v_s}\) at an angle \(\alpha\) to the line of sight (Figure 2) generates radio emission at frequency \(f\) with the frequency drift rate:
\begin{equation}\tag{1}
\frac{{df}}{{dt}}\approx\frac{{df}}{{dn}}\frac{{dn}}{{dr}}\frac{{{v_s}\cdot{v_{gr}}(r)}}{{{v_{gr}}(r) – {v_s}\cos\alpha}}
\end{equation}
where \({v_{gr}}(r) \) is the group velocity of the radio emission, and \(n(r) \) is the plasma density at the distance \(r\) from the Sun. When obtaining Equation (1), we assume that \({v_{gr}}({r_1}) = {v_{gr}}({r_2}) = {v_{gr}}(r) \) is satisfied if the distance between points \({r_1}\) and \({r_2}\) is small compared with the sizes of the inhomogeneities that lead to the observed changes of type III dynamic spectra. We also consider that the difference between travel times from points \({r_1}\) and \({r_2}\) to an observer is mainly defined by the distance \( {r_2} – {r_1} \approx \delta r \cdot \cos\alpha \) crossed by the electromagnetic wave (Figure 2). For fundamental radio emission the frequency \(f\) equals the local plasma frequency \(f = {f_{pe}} = {\omega _{pe}}/2\pi = \sqrt {{e^2}n/\pi m} \) (\(e\) is the electron charge and \(m\) is its mass), and in this case, \(df/dn = f/2n\). The source velocity \({v_s}\) is assumed to be equal to \({v_s} = {v_0}/2\), where \({v_0}\) is the velocity of fast electrons (Mel’Nik et al., 1999).
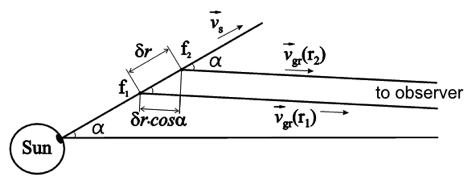
Figure 2. Type III exciter propagating at an angle \(\alpha\) to the line of sight.
In the plasma model of radio emission the fundamental radio emission (the electromagnetic wave \(t\)) appears at scattering of Langmuir waves by ions \(i\) \(l + i = t + i\). In these processes the electromagnetic wave frequency equals the Langmuir wave frequency \({\omega _t} = \sqrt {\omega _{pe}^2 + k_t^2{c^2}} = {\omega _l} = \sqrt {\omega _{pe}^2 +3k_l^2v_{Te}^2}\) (here \({k_t}\) is the wave number of electromagnetic wave, \({v_{Te}}\) is the thermal velocity of electrons). From this equation, we conclude that electromagnetic waves concentrate mainly at wave numbers \({k_{t,0}} \approx \sqrt 3 {k_{l,0}}{v_{Te}}/c\) and their group velocity \({v_{gr}} = {\left. {\frac{{\partial {\omega _t}}}{{\partial {k_t}}}} \right|_{{k_{t,0}}}} = {k_{t,0}}{c^2}/{\omega _t}\) is
\[{v_{gr}}=\sqrt3\frac{{{v_{Te}}c}}{{{v_0}}} \tag{2}\]
Then the frequency drift rate in Equation (1) is positive for
\[{v_{gr}}<{v_s}\cos\alpha \tag{3}\]
if electrons move outward from the Sun, i.e. \(dn/dr < 0\). Taking into account Equation (2), the condition in Equation (3) can be rewritten as
\[{v_0}>\sqrt{\frac{{2\sqrt3{v_{Te}}c}}{{\cos\alpha}}}\tag{4}\]
For electrons moving toward the observer (\(\alpha=0\)) we find for the critical velocity \(v_0^*\) that
\[v_0^*=\sqrt{2\sqrt3{v_{Te}}c}\;, \tag{5}\]
which gives \(v_0^*=7\cdot {10^9}~\mbox{cm/s}\) for plasma temperature \({T_e}=2\cdot{10^6}\) K. If we assume that the source velocity remains constant while propagating through the coronal plasma, the observed type III bursts with changing drift-rate signs can be understood in the following way: Fast electrons with velocities lower than \(v_0^*\) generate type III bursts with negative drift rates. When they enter the regions, in which the plasma temperature is low enough for \({v_0}>v_0^*\) the fast electrons generate type III bursts with a positive drift rate (the frequency band of 18-32 MHz type III burst observed on August 25, 2012). When they enter high-temperature regions in which \({v_0}<v_0^*\), the type III bursts will again display negative drift rates (the frequency band of 18-32 MHz for the same burst). Thus the observation of type III bursts with a change in the drift-rate sign means that the corresponding electron beams pass through regions of different temperatures.
Conclusion
In addition to normal type III bursts and fast type III bursts (Melnik et al. 2008), type III bursts with a changing sign of their drift rates are observed in the decameter range. In this wave band such bursts are rare, while in the decimeter range such type III bursts are common. The nature of these phenomena in the decimeter and decameter ranges can be different. Even assuming that decimeter type III bursts with changing drift-rate signs result from the simultaneous propagation of fast electrons toward and away from the Sun, the explanation of decameter type III bursts encounters difficulties. Because both fluxes and drift rates of these unusual decameter type III bursts are similar to those for standard type III bursts, we assumed that the change of the drift-rate sign in these bursts is connected with the properties of the plasma through which the electrons propagate. If the velocity of the source is lower than the group velocity of the type III radio emission, bursts with negative drift rates are observed. Otherwise, type III bursts have positive drift rates. When these velocities are approximately equal, fast type III bursts are recorded. Thus, from this point of view, all types of decameter type III bursts – standard, fast and with a changing sign of drift rates – can be understood. Moreover, because of the critical velocity for sign change, which is defined by the plasma temperature, we can determine the heights of regions with different temperatures.
References
Melnik, V.N.; Brazhenko, A.I.; Konovalenko, A.A.; et al.: 2015, Sol. Phys., 290, 193
Mel’Nik, V. N.; Konovalenko, A. A.; Rucker, H. O.; et al.: 2008, Sol. Phys., 250, 133
Mel’Nik, V. N.; Lapshin, V.; Kontar, E., 1999, Sol. Phys., 184, 353
*Complete list of authors: Valentin Melnik, Anatoliy Brazhenko, Alexander Konovalenko, Carine Briand, Vladimir Dorovskyy, Philippe Zarka, Anatoliy Frantsuzenko, Helmut Rucker, Boris Rutkevych, Myhailo Panchenko, Loran Denis, Teimuraz Zaqarashvili and Bidzina Shergelashvili
