Narrowband dm-spikes belong to the most interesting fine structures of solar radio bursts that are closely connected to primary flare energy-release processes (Krueger 1979) and observed in some cases near the Type III burst starting frequency. They occur in clouds of narrowband bursts with a typical duration less than 100 ms, frequency relative bandwidth 1-3 %, and brightness temperature up to $10^{15}$ K.
For them several radio emission models were suggested. Earlier models suggested emission by the electron cyclotron maser mechanism for $Y=\omega_{pe} / \omega_{ce} < 1$, where $\omega_{pe}$ is the electron plasma frequency, $\omega_{ce}$ is the electron cyclotron frequency (Melrose & Dulk 1982). In this model, emission occurs near the harmonics of the electron cyclotron frequency. However, non-integer ratios between spike bands were observed by Krucker & Benz (1994). Therefore, a model based on emission at Bernstein mode frequencies was proposed by Willes & Robinson (1996). Moreover, the model of emission at upper-hybrid frequencies was suggested for $Y > 1$ by Stepanov et al. (2001). In this model, emission regions are separated in height, and thus they emit at separate frequencies.
We investigate the 2013 November 7 spike event showing unique very narrow bands with non-integer frequency ratios. In interpretation of this event we consider two models: (1) with the emission from one emission source at Bernstein mode frequencies and (2) with the emission from separated emission sources at upper-hybrid frequencies.
Observation
We study the 2013 November 7 spike event where spikes were clustered in unique very narrow bands (Figure 1). This spike event belongs to 53 spike events that were registered by Ondřejov radiospectrographs in the range 0.8-2 GHz during 1992-2020 years. The frequencies of its four narrow bands are 1003, 1276, 1572, and 1877 MHz, giving ratios between adjacent bands as 1.275, 1.23, and 1.19. Figure 2 shows the radio flux evolution of these bands and their cross-correlations.
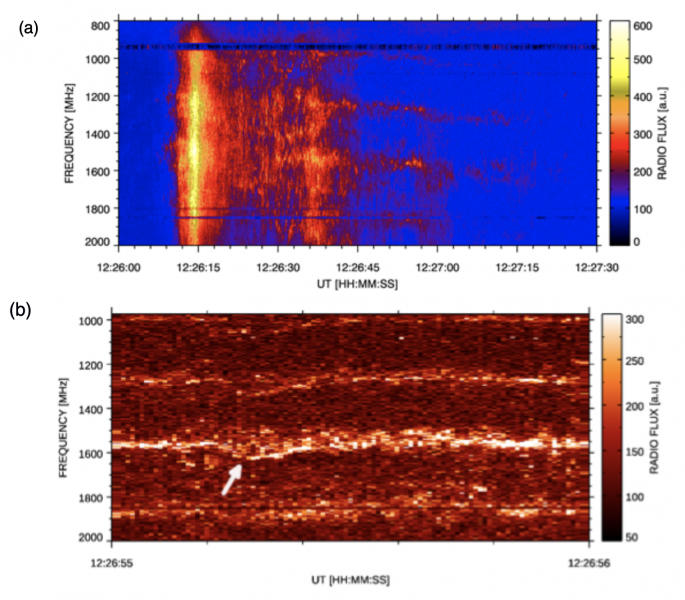 Figure 1 – Observed spike event on 2013 November 7. (a) Broadband cloud of spikes followed by unique four very narrow bands of spikes. (b) Detail of the radio spectrum in 1 – 2 GHz range with 1 s duration. The arrow shows the band frequency variation for which the form is synchronized with the similar forms in all four bands. The spectrum is not smoothed and thus shows bins in the record.
Figure 1 – Observed spike event on 2013 November 7. (a) Broadband cloud of spikes followed by unique four very narrow bands of spikes. (b) Detail of the radio spectrum in 1 – 2 GHz range with 1 s duration. The arrow shows the band frequency variation for which the form is synchronized with the similar forms in all four bands. The spectrum is not smoothed and thus shows bins in the record.
Results
We computed growth rates for both our models. For the Bernstein model (Figure 3), we found the corresponding Bernstein modes cross regions of positive growth rates. Moreover, these modes have a non-integer frequency ratios, and their positions fit well with the observed band frequencies. The parameters in this model correspond to the plasma density $9 \times 10^{9}$ cm$^{-3}$ and magnetic field strength 113 G. In the upper-hybrid model, we also estimated growth rates (Figure 4). The corresponding plasma density and magnetic field strength are in the range $1.1 – 2.9 \times 10^{10}$ cm$^{-3}$ and 119-111 G, respectively.
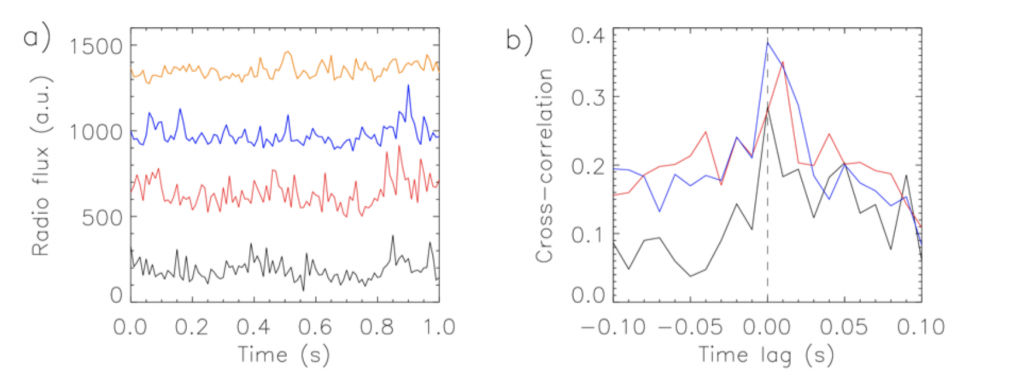 Figure 2 – (a) Evolution of radio flux at 1877 MHz (black line), at 1572 MHz (red line) +400 au, at 1276 MHz (blue line) +800 au, and at 1003 MHz (orange line) +1200 au, starting at 12:26:55 UT and lasting 1 s. (b) Cross-correlations of the radio flux profiles on 1877 and 1572 MHz (black line), 1572 and 1276 MHz (red line), and 1276 and 1003 MHz (blue line).
Figure 2 – (a) Evolution of radio flux at 1877 MHz (black line), at 1572 MHz (red line) +400 au, at 1276 MHz (blue line) +800 au, and at 1003 MHz (orange line) +1200 au, starting at 12:26:55 UT and lasting 1 s. (b) Cross-correlations of the radio flux profiles on 1877 and 1572 MHz (black line), 1572 and 1276 MHz (red line), and 1276 and 1003 MHz (blue line).
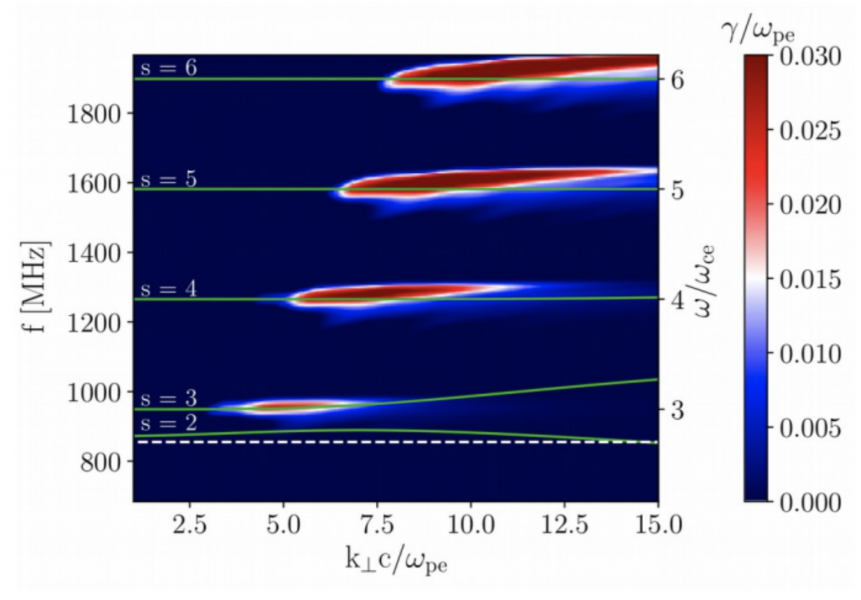 Figure 3 – Growth rates of the Bernstein modes as a function of the frequency and perpendicular wavenumber for parameters $\omega_{pe}/\omega_{ce} = 2.7$, $f_{pe} = 855$ MHz, $v_{tb}/c = 0.02$, $v_{t}/c = 0.25$, $n_{e}/n_{h} = 10$. Frequency corresponds to the radio emission on Bernstein mode frequencies. Green lines: dispersion modes, $s$ is the gyro-harmonic number of each branch. White dashed horizontal line denotes the plasma frequency.
Figure 3 – Growth rates of the Bernstein modes as a function of the frequency and perpendicular wavenumber for parameters $\omega_{pe}/\omega_{ce} = 2.7$, $f_{pe} = 855$ MHz, $v_{tb}/c = 0.02$, $v_{t}/c = 0.25$, $n_{e}/n_{h} = 10$. Frequency corresponds to the radio emission on Bernstein mode frequencies. Green lines: dispersion modes, $s$ is the gyro-harmonic number of each branch. White dashed horizontal line denotes the plasma frequency.
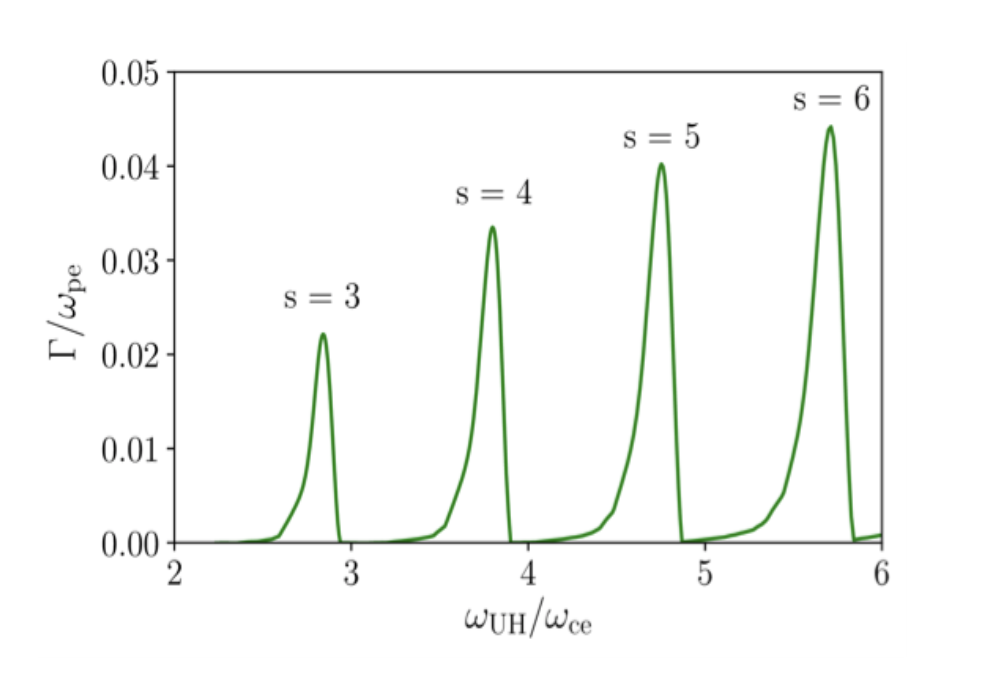 Figure 4 – Growth rate of the upper-hybrid waves vs. the upper-hybrid to electron cyclotron frequency ratio; $s$ denotes the gyro-harmonic number of the most unstable wave.
Figure 4 – Growth rate of the upper-hybrid waves vs. the upper-hybrid to electron cyclotron frequency ratio; $s$ denotes the gyro-harmonic number of the most unstable wave.
Conclusions
We found that the Bernstein mode model better explains the observed spikes than the upper-hybrid model, at least in the studied event. It fits very well with the observed frequencies for reasonable plasma parameters and produces well the observed band frequency difference of 300 MHz. Moreover, it is not very probable that four separated regions give these ratios in the upper-hybrid model. Another argument against upper-hybrid model is that it requests Alfvén speed $\sim 200.000$ km s$^{-1}$ to obtain $\leq 0.01$ s cross-correlation time lag between frequency bands (Figure 2b) when we assume typical density scale height in the corona.
Based on the recent paper
Karlický, M., Benáček, J., & Rybák, J. 2021, ApJ, 910, 108.doi:10.3847/1538-4357/abe62b
References
Krucker, S. & Benz, A. O. 1994, A&A, 285, 1038.
Krueger, A. 1979, Geophysics and Astrophysics Monographs, Dordrecht: Reidel, 1979
Melrose, D. B. & Dulk, G. A. 1982, ApJ, 259, 844. doi:10.1086/160219
Stepanov, A. V., Kliem, B., Krüger, A., et al. 1999, ApJ, 524, 961. doi:10.1086/307835
Willes, A. J. & Robinson, P. A. 1996, ApJ, 467, 465. doi:10.1086/177620
*Full list of authors: Marian Karlický, Jan Benáček and Ján Rybák
