There is ongoing discussion in the literature about the nature of zebra-structure (ZS) in type IV radio bursts (Chernov, 2011). We showed the possibility of a model with whistler waves to explain many thin components of ZS stripes, taking into account the effects of scattering of the whistlers on fast particles. Here, we show some complex examples of observations of ZS bursts in different wave ranges, which are difficult to interpret within the framework of the Double Plasma Resonance (DPR) mechanism. Then we pass directly to theoretical problems.
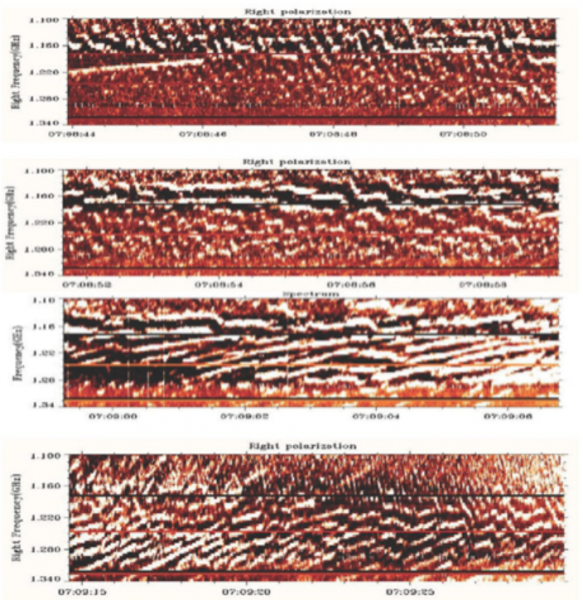 Figure 1. This dynamic spectrum shows the evolution of zebra-type bursts during 46 s, observed on 2004, December 1 with the Huairou radio station (Beijing). Initial fiber-type bursts transform into zebra patterns, as well as into decimetric millisecond spikes (from Chernov et al. 2017, Geo. and Aer. 57, 738).
Figure 1. This dynamic spectrum shows the evolution of zebra-type bursts during 46 s, observed on 2004, December 1 with the Huairou radio station (Beijing). Initial fiber-type bursts transform into zebra patterns, as well as into decimetric millisecond spikes (from Chernov et al. 2017, Geo. and Aer. 57, 738).
In the DPR model all the changes of ZS stripes are usually associated with changes of the magnetic field and with propagating fast magneto-acoustic waves. In a very complicated case the simultaneous presence of fast particles in a radio source with several different distribution functions was proposed (Zheleznyakov et al. 2016). However, the DPR conditions cannot change up to ten times per second and the complex zebra behavior, e.g. in Figure 1, cannot be explained by such changes (especially when the zebra is observed in the pulsating regime).
The basic condition of the instability (the existence of DPR levels, if the scale of the magnetic field heights $L_B$ is much smaller than the scale of the plasma density heights $L_N$) seems obvious: at different DPR levels, where the upper hybrid frequency \(\omega_{UH}\) becomes equal to the integer of electronic cyclotron harmonics $s\omega_{Be}: \omega_{UH} = (\omega_{Pe}^2 + \omega_{Be}^2)^{1/2} = s\omega_{Be}$ (Zheleznyakov, Zlotnik, 1975). However, the use of hypothetical schemes of dependencies of cyclotron frequency harmonics $s\omega_{Be}$ and the plasma frequency $\omega_{Pe}$ as functions of the coordinate x without digital scales on the axes, immediately raised questions, both in the first papers and in many subsequent ones, including the last review by Zheleznyakov et al. (2016) (see e.g. Figure 3 from the last review). Then, Karlický and Yasnov (2015) showed that microwave zebras are preferentially generated in the regions with steep gradients of the plasma density as for example in the transition region, using the density model by Selhorst, et al. (2008). The narrow peak in the hybrid band in the calculations of the growth rate of plasma waves at the upper hybrid frequency was received with zero velocity dispersion, it was missed as the infinitesimal quantity. The DPR resonance condition is only valid in the zero-temperature limit. The number of works devoted to the improvement of the DPR mechanism continues to grow. A major contribution to this improvement was made by Karlický with co-authors. Benáčhek, Karlický,Yasnov (2017) analyzed effects of temperatures of phone plasma and hot electrons on zebra generation processes. They showered that for a relatively low temperature of the hot electrons (the thermal velocity of hot electrons $v_t = 0.1c$) the dependence of the growth-rate vs. the ratio of the electron plasma and electron cyclotron frequencies expresses distinct peaks (for three first harmonics) and with increasing this temperature ($ v_t = 0.2c$) these peaks are smoothed. Moreover, as seen there in Fig. 4, also the relative bandwidth of the growth rate maxima increases with the increase of the harmonic s.
Such a behavior differs crucially from qualitative estimations shown previously (Zheleznyakov et al. (2016)).
At the same time, in the whistler model all the aforementioned properties of ZS stripes mentioned above were explained by real physical processes occurring during the coalescence of Langmuir waves (l) with whistler waves (w): $l + w \Rightarrow t$ (Chernov, 2006). First of all, a radio source of ZS is usually located in magnetic islands after CME ejections. Therefore the close connection of ZS with fiber bursts is simply explained by the acceleration of fast particles in magnetic reconnection regions in the lower part and in the upper part of magnetic islands. Let us recall that wavelike or saw-tooth frequency drift of stripes was explained by the switching of whistler instability from the normal Doppler cyclotron resonance into the anomalous one, qualitatively shown in Figure 2 for the distribution function F (Chernov, 1990).
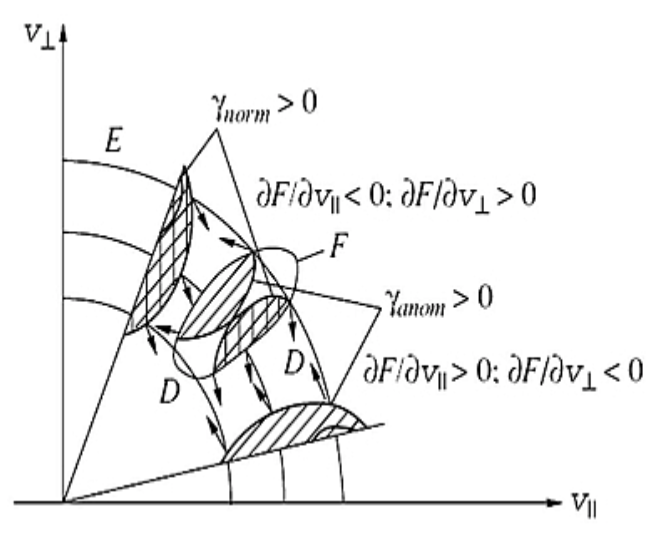
Figure 2. Switching instability of whistlers from the normal Doppler effect to anomalous one, according to Gendrin, 1981; F – levels of a distribution function, E – levels of equal energy, D – electron diffusion directions (from Chernov, 1990). In the model with the whistlers many components of the dynamics of the ZS stripes are explained by the quasi-linear effects of the diffusion of whistlers on fast particles. The smooth switching of the predominant contribution from the anomalous to normal Doppler resonances (and inversely) occurs in accordance with the sign of an operator $\Lambda$ in the growth rate expression (Gendrin, 1981; Bespalov and Trahtengerts, 1980):
\[ \Lambda=\frac{s\omega_B}{\omega V_\bot} \frac{\partial}{\partial V_\bot}+\left. \frac{k_\|}{\omega} \frac{\partial}{\partial V_\|} \right| _{ V_\| =(\omega – s\omega_B)/k_\|}\] It is known that in the normal Doppler effect, particles and wave propagate in the same direction, but in the anomalous Doppler effect, they propagate in opposite direction. This effect provide a smooth change of the whistler propagation direction and, consequently, a smooth change of the frequency drift of stripes. This effect is called a fan instability in the tokomak plasma (Parail and Pogutse, 1981). Such switching should lead to a synchronous change of the frequency drift of stripes and spatial drift of the radio source. New injections of fast particles cause sharp change in frequency drift of stripes in instantaneous ZS columns. Low frequency absorptions (black stripes of ZS) are explained by weakening of plasma wave instability due to the diffusion of fast particles by whistlers.
The superfine structure is generated by pulsating regime of whistler instability with ion-sound waves (Chernov et al. 2003). Rope-like chains of fiber bursts are explained by periodic whistler instability between two fast shock fronts in a magnetic reconnection region (Chernov, 2006). In the whistler model zebra-stripes can be converted into fiber bursts and spikes (and back) as it is shown in Figure 2.
This situation stimulates the search for new mechanisms. For example, earlier we showed the importance of explosive instability, at least, for the large flares with the ejections of protons. In the system the weakly relativistic beam of protons – nonisothermic plasma the slow beam mode of space charge possesses negative energy, and in the triplet slow and fast beam modes and ion-acoustic wave the explosive cascade of the harmonics of ionic sound is excited. The electromagnetic waves in the form of ZS stripes appears as a result of the fast protons scattering on these harmonics. Such a mechanism can also be promising for a ZS in the radio emission of the pulsar in the Crab nebula.
We discussed the difficulties of the DPR mechanism according to the latest publications and showed the potential of some promising alternative mechanisms.
For a comprehensive discussion of comparative analysis of observations of ZS and fiber bursts and different theoretical models we refer the reader to the reviews of Chernov (2012; 2016) (freely available at http://www.izmiran.ru/~gchernov/).
Based on the recent paper: G.P.Chernov, Chapter IV in book «Research advances in astronomy», Ed. N.Mehler, Nova Sience Publishers, New York, 2018, pp. 119_146. ISBN: 978-1-53614-098-9 See also: https://arxiv.org/abs/1807.08818
References
Benáček J., Karlický M., Yasnov L.V. (2017) Temperature dependent growth rates of the upper-hybrid waves and solar radio zebra patterns. Astron. Astrophys. 598, A108. https://doi.org/10.1051/0004-6361/201629395.
Chernov, G.P. (1990) Whistlers in the solar corona and their relevance to fine structures of type IV radio emission. Solar Phys.130. 75−82.
Chernov, G.P. 2011, Fine structure of solar radio bursts, Springer ASSL 375, Heidelberg.
Fomichev V.V., Fainshtein, S.M. and Chernov, G.P. (2009) A Possible Interpretation of the Zebra Pattern in Solar Radiation. Plasma Phys. Rep. 35, 1032-1035. DOI: 10.1134/S1063780X09120058.
Zheleznyakov, V.V., Zlotnik, E. Ya., Zaitsev, V. V., and Shaposhnikov, V. E. (2016) Double plasma resonance and its manifestations in radio astronomy. Physics-Uspekhi, 59, N.10, 997-1020. https://doi.org/10.3367/UFNe.2016.05.037813
