We study the influence of kinetic-scale Alfvénic turbulence on the generation of plasma radio emission in the solar coronal regions where the plasma/magnetic pressure ratio $\beta $ is smaller than the electron/ion mass ratio $m_{e}/m_{i}$. The present study is motivated by the phenomenon of solar type I radio storms associated with the strong magnetic field of active regions. The measured brightness temperature of the type I storms can be up to $\leq 10^{10}$ K for continuum emission, and can exceed $10^{11}$ K for type I bursts. At present, there is no generally accepted theory explaining such high brightness temperatures and some other properties of the type I storms.
Theory
We propose the model with the imbalanced turbulence of kinetic-scale Alfvén waves producing an asymmetric quasilinear plateau on the upward half of the electron velocity distribution, $\sqrt{1+T_{i}/T_{e}}V_{Te}<V_{\parallel }<V_{A}$ (see Figure 1). Here $T_{i}/T_{e} $ is the ion to electron temperature ratio, $V_{Te}$ is the electron thermal velocity, $ V_{A}$ is the Alfvén velocity and $V_{\parallel }$ is the electron velocity component parallel to the mean magnetic field $\vec{B}_{0}$.
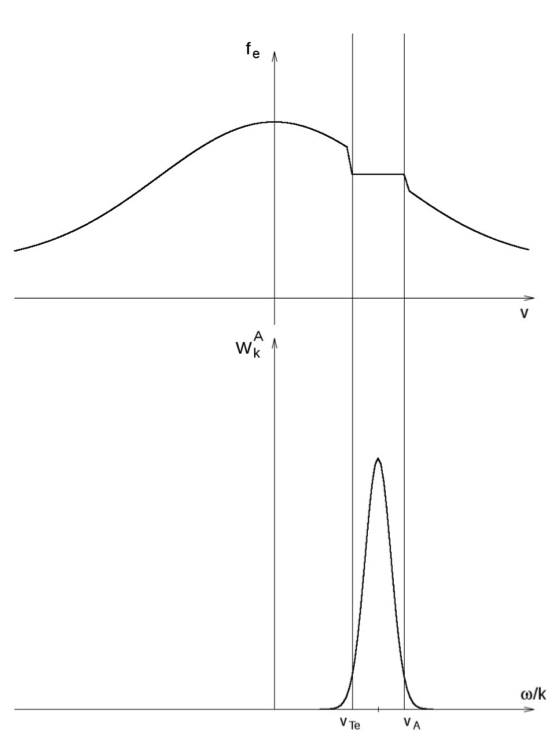
Figure 1. Illustration of the time-asymptotic electron velocity distribution $f_{e}$ modified by the IAW spectrum $W_{k}^{A}$. The quasilinear diffusion establishes a plateau on the initially Maxwellian distribution in the resonant velocity range $\sqrt{1+T_{i}/T_{e}}V_{Te}<V_{\parallel }<V_{A}$. Outside this interval the velocity distribution remains Maxwellian.
We are interested in the regions where the plasma $\beta $ can be smaller than the electron to ion mass ratio $m_{e}/m_{i}$. In such a low-$\beta $ plasma the short scale Alfvén waves are inertial Alfvén waves (IAWs), and phase velocities are larger than the electron thermal velocity $V_{Te}$.
Such local flattening of the velocity distribution suppresses the Landau damping of the resonant Langmuir waves (LWs), making possible their spontaneous growth to high nonthermal levels. In Figure 2 the normalized spectral energy density of Langmuir waves $W_{k}^{l}/W_{th}^{l}$ in the resonant wavenumber range $V_{Te}/V_{A}<k\lambda _{De}<0.82$ is shown.
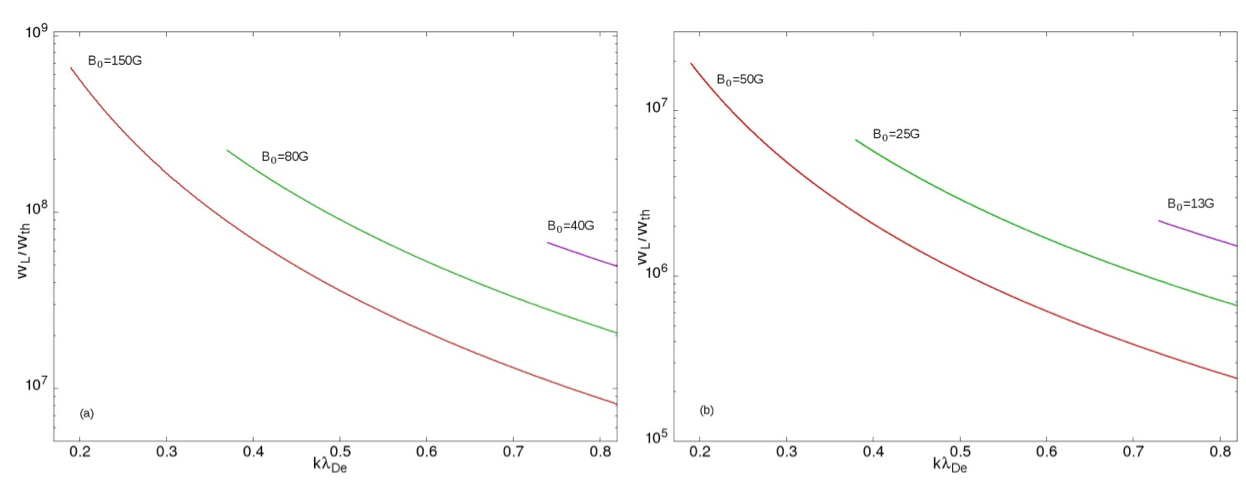
Figure 2. Normalized spectral energy density of Langmuir waves in the resonant wavenumber range $V_{Te}/V_{A}<k\lambda _{De}<0.82$. The plasma parameters are $n_{0}=2.8\times 10^{8}$ cm$^{-3}$; $T_{i}/T_{e}=0.5$. Case (a) corresponds to $T_{e}= 10^{6}$ K and three values of magnetic field strength $B_0 = 150$, $80$ and $40$ G. Case (b) corresponds to $T_{e}= 10^{5}$ K and three values of magnetic field strength $B_0 = 50$, $25$ and $13$ G.
We have considered two types of possible coronal plasma parameters for the heliocentric distances $R/{\mathrm R_{\odot }}\approx 1.1$ with electron density $n_{0}=2.8\cdot 10^{8}$ cm$^{-3}$ or $f_{pe}=150$ MHz (Warmuth and Mann, 2005). The first one with $T_{e}=10^{6}$ K and stronger magnetic field in the range $B_{0}=150$–$40$ G (Figure 2a). The second one with lower temperature $T_{e}=10^{5}$ K and weaker magnetic field in the range $B_{0}=50$–$13$ G (Figure 2b). As is seen from Figure 2, the normalized spectral energy density of LWs reaches its maximum value
\[
W_{k}^{l}/W_{th}^{l}\simeq 6\cdot 10^{8},
\]
for $B_{0}=150$ G, $T_{e}=10^{6}$ K and
\[
W_{k}^{l}/W_{th}^{l}\simeq 2\cdot 10^{7},
\]
for $B_{0}=50$ G, $T_{e}=10^{5}$ K for the resonant velocities of LWs close to the upper boundary, $V_{LW}\lesssim V_{A}$, which correspond to LW wavenumbers $k\lambda _{De}\gtrsim 0.19$. For lower values of magnetic field strength the normalized spectral energy density of LWs is still high, whereas the resonance wavenumber range becomes narrower.
The resulting high-amplitude LWs can interact non-linearly with low-frequency plasma waves generating electromagnetic radiation (radio waves) close to the local plasma frequency. We have considered the theory of fundamental plasma emission generated by the nonlinear fusion $L+S\rightarrow T$, and/or decay $L\rightarrow T+S$. Here $L$ is the Langmuir wave, $S$ is the ion sound wave and $T$ is the transverse radio wave. The estimation of saturation level for fundamental plasma emission by the fusion/decay processes $L\pm S\rightarrow T$ shows that even with the unfavorable thermal level of ion-sound waves, the brightness temperature of radio emission in our model is $T_{T+}\approx 10^{9}$–$10^{11}$ K, $T_{T-}\approx 10^{12}$–$10^{15}$ K (for $T_{e}=10^{6}$ K) and $T_{T+}\approx 10^{8}$–$10^{10}$ K, $T_{T-}\approx 5\cdot 10^{9}$–$10^{12}$ K (for $T_{e}=10^{5}$ K), which is high enough to explain observations. The bursts with extremely high brightness temperatures $\gtrsim $ $10^{11}$ K can be easier generated by the decay process.
Final remarks
We investigated the influence of imbalanced small-scale IAW turbulence on the spontaneous growth of LWs. The resulting high-amplitude LWs can generate type I radio emission observed above the active regions in the solar corona.
Our estimations show that even with the thermal-level ion-acoustic waves, we get the observed brightness temperature for type I emission. The harmonic emission is never observed in type I storms; it does not occur also in our model, because the back-scattered LWs meet a strong Landau damping, $\gamma_{L}\approx \omega _{pe}$.
Additionally, the current model reproduces the almost $100\%$ polarization in the o-mode of type I bursts. The main reason is that the frequency of the emission due to the $L\pm S\rightarrow T$ processes is below the cutoff frequency of the extraordinary (x-) mode, $\omega_{\mathrm x}=[\omega_{Be}+(\omega_{Be}^2+4\omega_{pe}^2)^{1/2}]/2$ for the values of the ratio, $\omega_{Be}/\omega_{pe}$, required in our model. The resulting electromagnetic emission then must be $100\%$ in the o-mode.
Our model works in low-beta plasmas, where the Alfvén velocity exceeds the electron thermal speed ($V_{A}>V_{Te}$). Such conditions can be found in the solar corona at radial distances $\approx 1.1$ solar radii, where type I storms are generated. Recent observations have demonstrated that magnetic fields above active regions at these distances can be strong enough, several $10$s of G, and temperatures low, down to $10^{4}$ K (see examples in Figure 8 by Schad et al. 2016 with instances of $B_{0}$ from $10$ to $150$ G, and paper by Antolin et al. 2015 with coronal $T_{e}$ from $10^{4}$ to $10^{6}$ K).
The often observed phenomenon of coronal rain provides a well-documented example of cold plasma patches created at high coronal levels by thermal instability (see Antolin et al. 2015, and references therein). Plasma in the upper parts of long magnetic loops is especially prone to this instability. As the type I emission is generated, tentatively, at the tops of the highest magnetic loops overlapping active regions, the relatively cold plasma, produced there by thermal instability, may provide a suitable conditions for type I radio emission.
*Full list of authors: O. Lyubchyk, E.P. Kontar, Y.M. Voitenko, N.H. Bian, D.B. Melrose
Based on a recently published article: O.Lyubchyk, E.P. Kontar, Y.M. Voitenko, N.H. Bian, D.B. Melrose., Solar plasma radio emission in the presence of imbalanced turbulence of kinetic-scale Alfvén waves, 2017, Solar Physics, 292 (9) DOI: 10.1007/s11207-017-1140-1.
Additional info
The full work can be accessed here: http://arxiv.org/abs/1707.02295
References
Antolin, P. et al. 2015, ApJ, 806, 81
Schad, T.A. et al. 2016, ApJ, 833, 5
Warmuth, A. and Mann, G. 2005, A&A, 435, 1123
