Inelastic scattering off moving or oscillating density fluctuations leads to broadening of radio signals propagating in the solar corona and solar wind. Using an anisotropic density fluctuation model from the kinetic scattering theory for solar radio bursts, we deduce the plasma velocities (perpendicular to the line of sight) required to explain observations of spacecraft signal frequency broadening. The kinetic energy associated with these inferred bulk velocities cascades to smaller and smaller scales, where it is ultimately dissipated through damping of ion-sound waves. The inferred energy deposition rate associated with this process compares very favorably with those required to heat the corona and drive the solar wind.
Inelastic Scattering of Radio Waves and Frequency Broadening Measurements
Considering a distant point source, Azzollini et al (2024) calculate the effects of inelastic scattering in the presence of motions perpendicular to the line of sight, and they derive the associated diffusion tensor for radio waves in anisotropic turbulent plasma. The frequency broadening rate (per unit travel distance along the direction of propagation $z$) is proportional to the square of the velocities in the two directions perpendicular to the line of sight. In anisotropic density turbulence (with a constant anisotropy factor $\alpha$, with values of $\alpha<1$, corresponding to fluctuations preferentially aligned with the magnetic field), the effect of velocities in the direction of the solar radial is weighted by $\alpha^2$, so that such motions have a much smaller effect than motions that are transverse to the solar radius in the plane of the sky. These expressions can be integrated along the line of sight to give the frequency broadening $\Delta f$ observed at the Earth, which can be compared with observations (left panel of Figure 1) to determine the average magnitude of the perpendicular velocities. The solid and dashed lines in the right panel of Figure 1 show the $\Delta f$ derived using the nominal density fluctuation spectrum (see Kontar et al. 2023 for details), for two different anisotropy factors: $\alpha=0.25$ (applicable to emission of radiation at the fundamental) and $\alpha=0.4$ (applicable to radiation at the second harmonic). (We consider both values of $\alpha$ because we do not a priori know whether we are observing fundamental or harmonic radiation.) The grey area shows the range in $\Delta f$ values obtained; the lower bound is determined by a density fluctuation amplitude of half the nominal expression of density fluctuations and an anisotropy factor $\alpha=0.25$, and the upper bound is determined by a density fluctuation amplitude of twice the nominal expression of density fluctuation and an anisotropy factor $\alpha=0.4$.
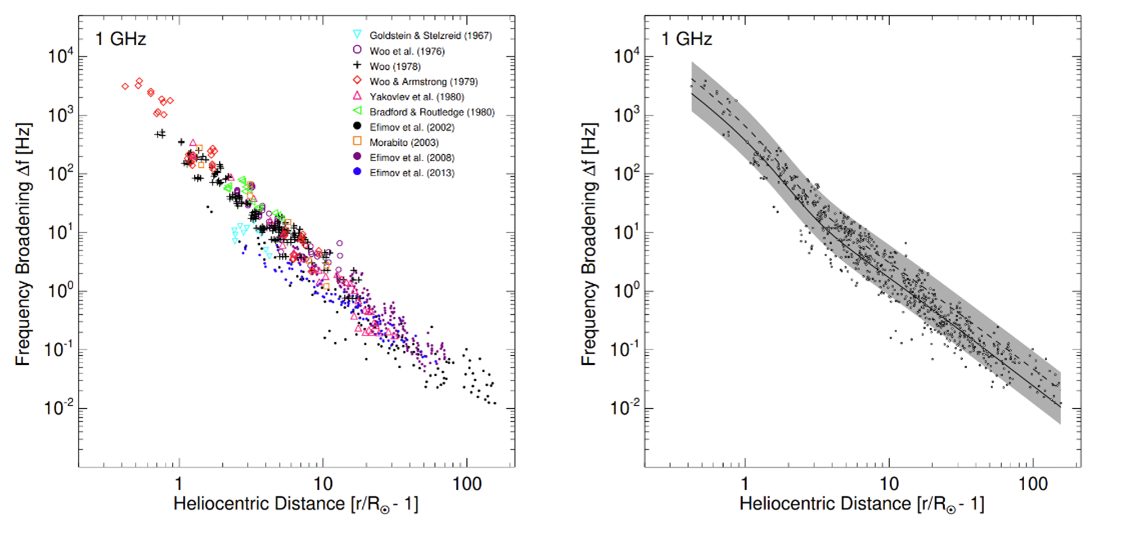
Figure 1. Left: Observed spectral broadening (the square root of the variance) of spacecraft signals observed through the corona from various studies, where each carrier signal is scaled to $f=1$ GHz using $\Delta f/f \propto 1/f^2$. Right: Derived form of $\Delta f$, for $v_{\perp}=30$ km s$^{-1}$ (determined from measurements of non-thermal line broadening), and $v_\parallel=\sqrt{v_s^2 + v_{\mathrm{sw}}^2}$, where $v_s$ is the sound speed and $v_{\mathrm{sw}}$ is the solar wind speed.
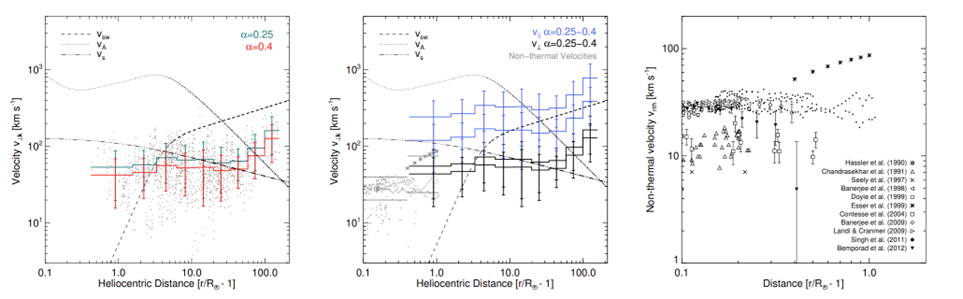
Figure 2. Left: Plane-of-sky velocity $v_{\perp}$ calculated using the frequency broadening measurements from Figure 1. The green and red points show the conversion of individual $\Delta f$ data points from Figure 1, for different values of $\alpha$, with binned averages and weighted uncertainties on each bin. Middle: Parallel and perpendicular velocities $v_{\parallel}$ (blue) and $v_{\perp}$ (black) required to solely explain the frequency broadening measurements in Figure 1. The grey dots and stars show a summary of the measured values of the non-thermal velocity standard deviation from the right panel. Also shown is the solar wind speed $v_{\mathrm sw}$, the ion-sound speed $v_s$, and the Alfvén speed $v_A$, obtained using the density and magnetic field models in Kontar et al. 2023. Right: $1\sigma$ non-thermal velocities $v_{\mathrm{nth}}$ from line-of-sight Doppler broadening of coronal lines.
Alfvén Wave Cascade and Damping of Ion-Sound Waves
Velocity fluctuations along the line of sight are often interpreted as manifestations of motions perpendicular to the magnetic field (Doyle et al. 1998), and similar motions in the plane of the sky lead to frequency broadening of radio signals. Such motions are commonly interpreted as Alfvén waves, which can undergo turbulent cascade to smaller scales (e.g., Holloweg 1978). The power per unit mass (erg g$^{-1}$ s$^{-1}$) available to be deposited through such a Kolmogorov cascade in strong MHD turbulence (Goldreich & Sridhar 1995) is estimated to be
\[ \epsilon_{\ell_\perp} \simeq \frac{ v_{\perp}^2 }{\tau} \simeq \frac{ v_{\perp}^3}{\ell_\perp}~, \]
where $\ell_\perp $ is a measure of the transverse correlation length (Hollweg 1986). Energy could be supplied to the corona and solar wind via absorption of the energy contained in the strongly damped parallel propagating ion-sound or slow magneto-sonic waves. The inferred energy deposition rate, integrated over the range of heights (2-3 $R_\odot$) (where it is most effective) corresponds to an energy flux $\sim 3 \times 10^5$ erg cm$^{-2}$ s$^{-1}$ (300 W m$^{-2}$). Such an energy flux is broadly consistent with that required to balance energy losses and heat the corona (see e.g., Withbroe 1988).
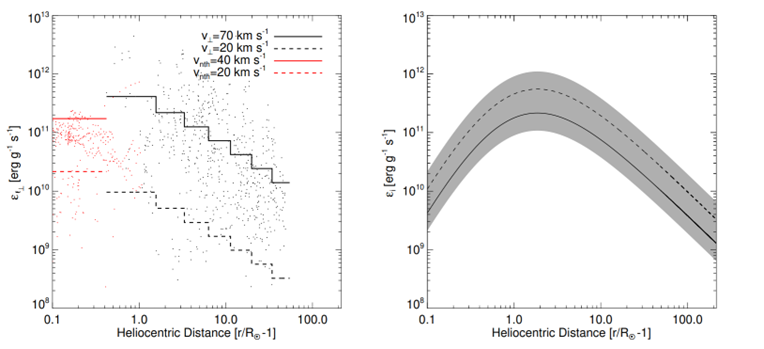
Figure 3. Left: Available power per unit mass (erg/g/s) using perpendicular velocity fluctuations from Figure 1. The solid and dashed lines correspond to the range (20-70) km~s$^{-1}$ (black) from frequency broadening measurements, and (20-40) km~s$^{-1}$ for $r < 1.4~R_\odot$ for non-thermal velocities from coronal lines (red). Right: Coronal heating rate per unit mass (erg/g/s) from Landau damping of ion-sound waves. The solid and dashed lines show the results for the nominal density fluctuation amplitude for anisotropy factors $\alpha=0.25$ and $\alpha=0.4$, and the grey area corresponds to the range of values from one-half to double the nominal density fluctuation amplitude, taking both values of $\alpha$ into account.
Conclusions
The inferred velocities are consistent with motions that are dominated by the solar wind at distances $\gtrsim 10~R_\odot$, but the levels of frequency broadening for $\lesssim 10 ~R_\odot$ require additional radial speeds of about 300 km s$^{-1}$ and/or transverse speeds of about (20-70) km s$^{-1}$. The inferred radial velocities also appear consistent with the sound or proton thermal speeds, while the speeds perpendicular to the radial direction are consistent with non-thermal motions measured via coronal Doppler-line broadening, interpreted as Alfvénic fluctuations. Landau damping of parallel propagating ion-sound (slow MHD) waves results in a proton heating rate that is comparable to the rates available from a turbulent cascade of Alfvénic waves at large scales, suggesting a coherent picture of energy transfer, via the cascade or/and parametric decay of Alfvén waves to the small scales where heating takes place.
Based on the recent paper by Francesco et al, Plasma Motions and Compressive Wave Energetics in the Solar Corona and Solar Wind from Radio Wave Scattering Observations, ApJ 968 72 (2024), DOI: 10.3847/1538-4357/ad4154
References
Doyle, J. G., Banerjee, D., & Perez, M. E. 1998, SoPh, 181, 91, doi: 10.1023/A:1005019931323
Goldreich, P., & Sridhar, S. 1995, ApJ, 438, 763, doi: 10.1086/175121
Hassler, D. M., Rottman, G. J., Shoub, E. C., & Holzer, T. E. 1990, ApJL, 348, L77, doi: 10.1086/185635
Hollweg, J. V. 1986, J. Geophys. Res., 91, 4111, doi: 10.1029/JA091iA04p04111
Kontar, E. P., Emslie, A. G., Clarkson, D. L., et al. 2023, ApJ, 956, 112, doi: 10.3847/1538-4357/acf6c1
Withbroe, G. L. 1988, ApJ, 325, 442, doi: 10.1086/166015
