The solar radio zebra patterns, or zebras, provide detailed diagnostics of plasma density and magnetic field in the corona. The zebras appear in radiograms during Type IV solar radio bursts as a series of parallel stripes that are narrow in frequency.

The main emission model of radio zebras relies on a double plasma resonance, a resonance between the plasma frequency, gyro-harmonic of the cyclotron frequency, and the frequency of unstable upper-hybrid (UH) electrostatic waves (Zhelezniakov & Zlotnik 1975,Chen et al. 2011).  The driver of the instability are superthermal electrons which are trapped in a flare loop and form a loss-cone distribution. During the instability, the UH waves grow and saturate. The electrostatic waves are then consequently converted to the observed electromagnetic waves by merging with low-frequency waves or scattering on plasma particles.

Assuming that individual stripes are generated at gyro-harmonics of the cyclotron frequency, very high gyro-harmonic numbers s are typically detected, s~50–150 (Karlický & Yasnov, 2021). In contrast, the theoretical models predict that the highest growth rates are obtained for relatively low gyro-harmonic numbers, s<10 (Benáček & Karlický, 2018).

Methods and Results

We consider a plasma consisting of two components: 1) dense thermal background plasma and 2) low-density loss-cone superthermal electrons characterized by their thermal parameter v_κ and Kappa loss-cone distribution with a loss-cone angle θ_c. We numerically calculated the growth rates of the UH waves as a weighted averages over the whole UH branch. We assumed that zebra stripes are formed when the growth rates form peaks.

Figure 1 presents the growth rates as functions of gyro-harmonic number for loss-cone angles θ_c = 30°–80°. For small angles θ_c = 30°–50°, the growth rates smooth with increasing gyro-harmonic number. However, for a large angle θ_c = 80°, the growth rates increase.

In addition, similar growth rate behavior also occurs when varying the thermal parameter of the loss-cone distribution v_κ (Figure 2), assuming θ_c = 80° is constant. For v_κ = 0.3 c, the values of growth rate peaks are approximately constant for all gyro-harmonic numbers, and the peaks smooth out. Nonetheless, for smaller thermal parameters v_κ = 0.15–0.25 c, the growth rates increase with increasing gyro-harmonic numbers, and the peaks, necessary for the formation of the Zebra pattern, are still formed.

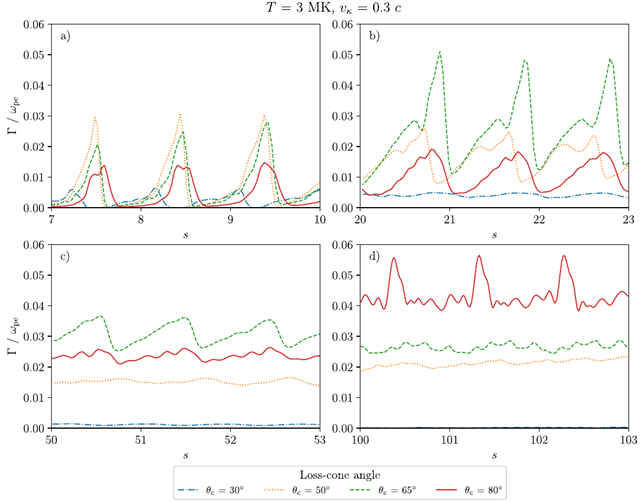
Figure 1: Average growth rates of the UH waves as a function of the loss cone angle θ_c for intervals: a) s = 7–10, b) s = 20–23, c) s = 50–53, and d) s = 100–103. Compare the blue and red lines for various s.

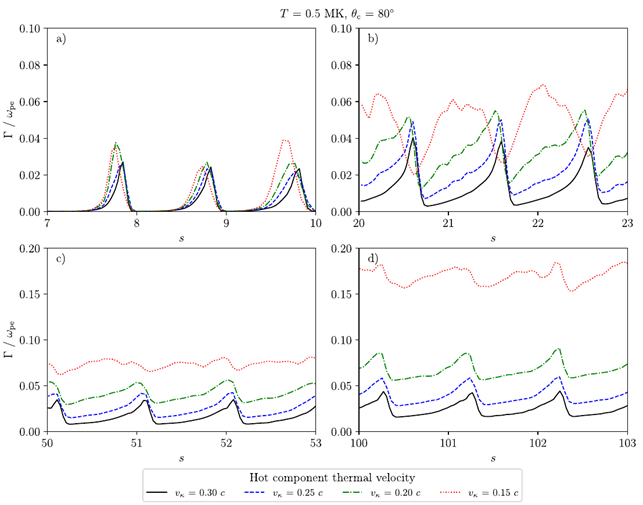
Figure 2: Similar as Figure 1, but for a dependence on the loss-cone thermal parameter v_κ. Compare the black and red lines for various s.

Conclusions

We found that the zebras with very high gyro-harmonic numbers, s~100, can be only formed for specific properties of the superthermal electrons ― very high loss-cone angles θ_c = 80° and relatively low thermal parameters v_κ < 0.3 c. Moreover, to fulfill the double-plasma resonance condition for high gyro-harmonic numbers, the plasma density in the zebra source needs to be high and the magnetic field strength relatively low.

Thus, we propose that zebras with high gyro-harmonic numbers could be generated in two regions:

1. In magnetic loops that are only slightly wider at their midpoints than at their footpoints. In such loops, only superthermal electrons with high pitch angles can be trapped (Krucker et al. 2020). Moreover, the plasma density in these loops needs to be high and the magnetic field strength relatively low.

In the region below the X-point of the magnetic reconnection in the standard flare model. Namely, it is expected that there is a plasma with high density and low magnetic field strength. However, for the zebra generation, the electron acceleration processes at the X-point and in collapsing magnetic trap in the plasma reconnection outflow need to produce the loss-cone distribution with a pitch angle of about  80°.

Based on a recent paper by Benacek & Karlicky, Zebra Stripes with High Gyro-Harmonic Numbers, Solar Physics 297:103 (2022),DOI: 10.1007/s11207-022-02036-y, ADS: 2022SoPh..297..103B

References:

Benáček, J. and Karlický, M.  2018, A&A, 611, A60.

Chen, B., Bastian, T. S., Gary, D. E., and Jing, J., 2011, ApJ, 736, 64.

Krucker, S., Masuda, S., White, S. M., 2020, ApJ, 894, 158.

Zhelezniakov, V.V. and Zlotnik, E.Ya., 1975, Sol. Phys., 44, 2, p.461-470.