We investigate angular broadening of radio wave scattering by density irregularities in the outer heliosphere and the very local interstellar medium (VLISM), incorporating an inner scale, latitudinal, and radial dependencies for the density fluctuation spectra and radiation propagation paths both near and out of the ecliptic plane.
Outer Heliospheric Radio Emission
Low-frequency radio wave emission was discovered in the distant heliosphere by the Voyager missions. A number of investigations [e.g., Gurnett et al., 1998] demonstrated that these radio emissions are apparently generated close to the boundary between the solar wind and the interstellar medium. Evidently, scattering by density irregularities plays a significant role in the propagation and angular broadening $\theta_{SC}$ of low-frequency 2 – 3 kHz radio emission (Cairns, 1995), especially radio wave intensity, angular size, propagation direction, and temporal and spectral variability.
Pickup Ion (PUI)-mediated high latitude fast Solar Wind vs Voyager Data in the Ecliptic Plane
The pickup ion (PUI)-mediated solar wind and the MHD turbulence transport model of Zank et al., 2018, that describes background solar wind, turbulence, and PUI properties from 1 AU to 84 AU, is used to evaluate density turbulence throughout the heliosphere. A simple scaling extends the theoretical predictions of the PUI model to the high latitude wind beyond the heliospheric termination shock (HTS). The near ecliptic solar wind and turbulence quantities are calculated using plasma and magnetometer data from the Voyager 2 (V2) spacecraft over the period 1977 to 2018. We observe noticeable differences in the high latitude and V2 plasma and magnetic field variables.
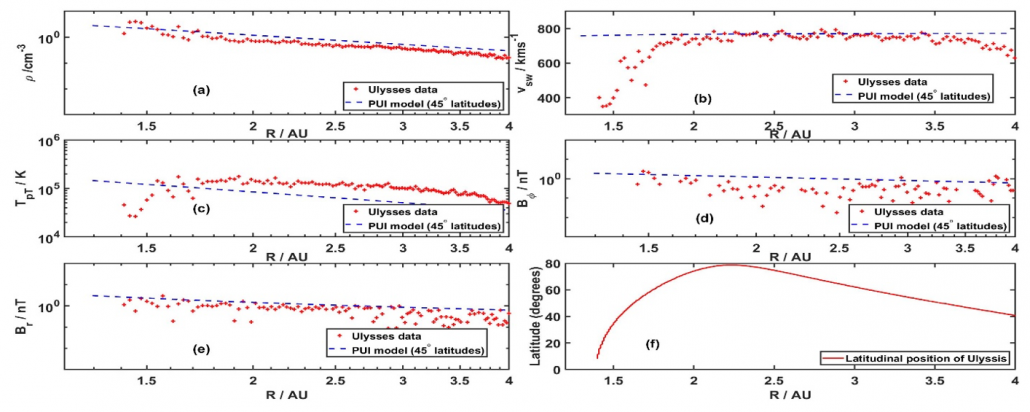
Figure 1 – Plots show (a) density, (b) solar wind speed, (c) proton temperature, (d) azimuthal magnetic field, (e) radial magnetic field, and (f) heliolatitude with increasing heliocentric distance over the period March 1, 1995 to March 31, 1996.
To check the consistency of the PUI model predictions, in Figure 1 we compare, the theoretical plasma parameters and magnetic field components derived at $45^\circ$ latitude with the Ulysses observations. We use Ulysses observations of plasma parameters at $0^\circ$ to $80^\circ$ latitudes. The figure shows similarities between Ulysses observations at high latitudes ($\gtrsim 40^\circ$) and PUI model predictions at $45^\circ$ latitude in radial profiles of the solar wind density, speed, and radial and azimuthal magnetic field components.
Inner Scale and Density Turbulence Amplitude
To estimate the inner scale $l_i$, we employ the Tasnim et al., 2020 inner scale model and the theoretical PUI model results and V2 data. We use $l_i = \beta l_u$ when $\beta l_u \geq r_{pg}$ and $l_i = 2\pi r_{pg}$ when $\beta l_u < r_{pg}$. Here, $l_u$ is the velocity correlation length, $r_{pg}$ is the thermal proton gyroradius and $\beta$ is the ratio between the inner scale and velocity correlation length. We estimate the value of $\beta$ based on the calculated length of the magnetic field fluctuation and the dissipation length scale of the magnetic field fluctuation. The inclusion of $l_i$ has a significant effect on the predictions of $\theta_{SC}$. Note that the correlation length controls the cascade rate (cascade rate $\propto l_u^{-1} \propto l_i^{-1}$) of turbulence.
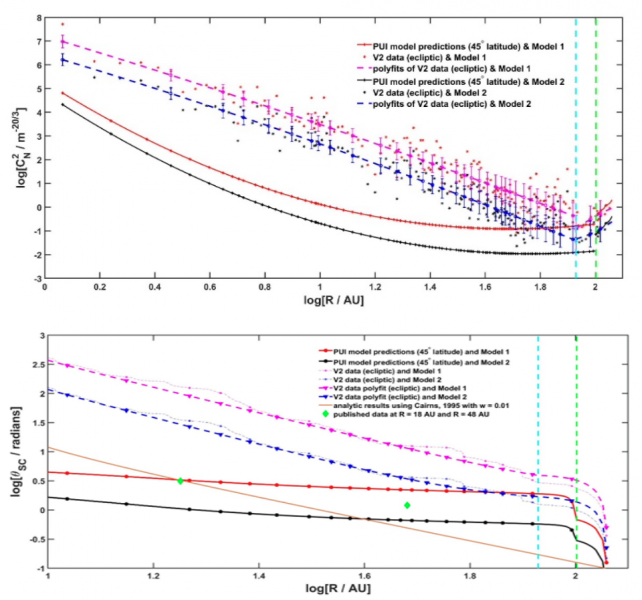
Figure 2 – Density turbulence amplitude $C_N^2$ as a function of radial distance from 1 AU to 118 AU at high latitude and in the near ecliptic plane. (Bottom panel) Radial variation of the angular broadening $\theta_{SC}$ derived from Equation 1 for the PUI mediated fast solar wind, the ecliptic slow solar wind, and estimates of the observed source size (green diamonds). Equation 1 includes inner scale effects. The analytic prediction for $\theta_{SC}$ by Cairns (1995) is overplotted in the figure.
Figure 2 (top) shows that the estimated $C_N^2$ (using two different approaches: described as model 1 and model 2) for the high latitude fast wind PUI model is much smaller than the $C_N^2$ calculated in the ecliptic plane using V2 observations. The difference in $C_N^2$ indicates that the variance of the density turbulence ${<\delta \rho>}^2$ is much larger in the ecliptic plane than that in the high latitude region. The larger ${<\delta \rho>}^2$ in the ecliptic slow solar wind than in the high latitude fast solar wind supports the suggestion of Armstrong et al. (2000) that density turbulence is weaker at high latitudes. The vertical cyan broken line shows the location of the HTS using the V2 data while the green dashed line identifies the assumed HTS location at high $45^\circ$ latitudes.
Angular Broadening of the Radio Source employing the Parabolic Wave Equation (PWE) Formalism
We apply the parabolic wave equation (PWE) theory to calculate the angular broadening of the radio waves due to scattering by density irregularities. We derive \[\theta_{SC}^2(R)=\pi^{-2}\Bigg[4\pi^2 r_e^2 \times \int^{R_{so}}_{R_{ob}}dR\frac{C^2_N(R)\lambda^{\alpha}_{fs} \Gamma(2-\frac{\alpha}{2})2^{2-\alpha} }{\big(1-\frac{f^2_{p0}(R)}{f^2}\big)\Gamma(\alpha/2)(\alpha-2) }q_i^{4-\alpha}\Bigg]^{\frac{2}{\alpha-2}}\]
The integral in the above equation is numerically solved for the density turbulence models. Based on the turbulence models and observations, we calculate the scattering angle of the radio sources in the high latitude and near ecliptic wind. Finally, we compare the numerical results with the analytic predictions from Cairns 1995 and the observed source sizes. In addition, Figure 2 (bottom) compares the predictions of $\theta_{SC}$ for the PUI-mediated high latitude solar wind with the apparent source size from Voyager 1 and 2 observations, finding good agreement between the observations and the theoretical predictions at high latitudes.
Conclusions
To summarize, our investigation provides an extended description of the angular broadening of outer heliospheric low frequency radio waves, addressing three essential factors: i) the inner scale, ii) the radially varying variance of density fluctuations that results in different radial profiles in the solar wind beyond 1 AU, and most importantly, iii) the contribution of the high latitude fast solar wind.
Based on recent paper by Tasnim et al., Density Turbulence and the Angular Broadening of Outer Heliospheric Radio Sources at High Latitudes and in the Ecliptic Plane, The Astrophysical Journal, 928, id.125, DOI: 10.3847/1538-4357/ac5031
References
Armstrong, J. W. , Coles, W. A., Rickett, B. J., J. Geophys. Res. 105 (2000): 5149-5156.
Cairns, I. Geophys. Res. Lett. 22, no. 24 (1995): 3433-3436.
Gurnett, D. A., Allendorf, S. C. ,Kurth, W. S. Geophys. Res. Lett. 25 (1998): 4433-4436.
Tasnim, S., Zank, G. P. , Cairns, I. H. , et al. Journal of Physics: Conference Series 1620, no. 1 (2020).
Zank, G. P., Adhikari, L., Zhao, L. -L., et al. Astrophys. J. 869, no. 1 (2018).
*Full list of authors: Samira Tasnim, Gary. P. Zank, Iver H. Cairns, and L. Adhikari
