Solar radio bursts of Type III were currently observed since decades in the interplanetary space (Reid and Ratcliffe, 2014). They result from a series of successive processes arising in solar coronal and wind plasmas where Langmuir wave turbulence is radiated by electron beams generated during flares, leading ultimately to the emission of electromagnetic waves at the fundamental plasma frequency $\omega _{p}$ and its second harmonic.
The Letter by Krafft and Savoini, 2022 presents two-dimensional Particle-In-Cell simulations showing for the first time the radiation, in randomly inhomogeneous plasmas, of electromagnetic waves emitted at $\omega _{p}$ by Langmuir wave turbulence generated by a weak electron beam, in conditions relevant to Type III solar radio bursts. These simulations use a panel of physical and numerical parameters that were not reached in previous works and take into account the presence of self-consistently varying random plasma density fluctuations (Celnikier et al., 1983, Krupar et al., 2018) in an exceptionally large and well resolved simulation box.
The Letter shows for the first time the essential impact of random density fluctuations of average levels $\Delta N$ of a few percent of the background plasma on the characteristics of the electromagnetic emission at the fundamental plasma frequency $\omega _{p}$. It demonstrates that actually not only wave nonlinear interactions contribute to the generation of such emissions, but also processes of Langmuir waves’ transformations on the fluctuating inhomogeneities.
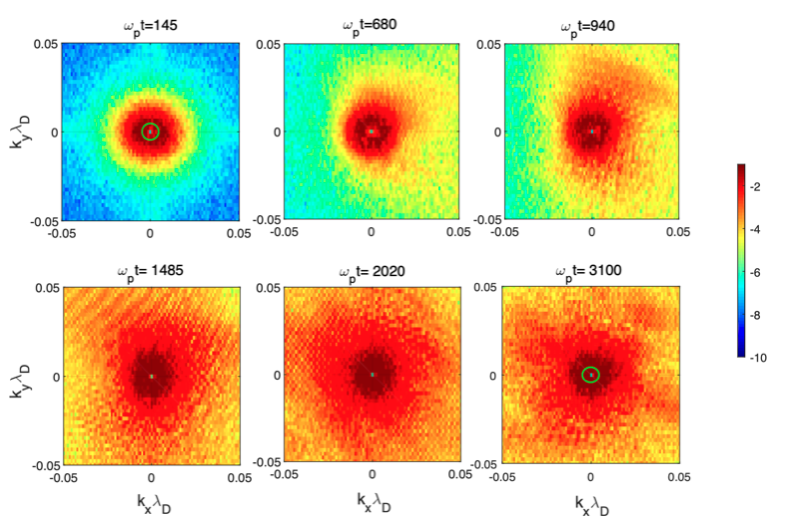Figure 1 – Distributions of the magnetic wave spectral energy density $\log_{10}(|B_{zk}(k_{x},k_{y})|^{2})$ emitted around the frequency $\omega _{k}\simeq \omega _{p}$, for $\Delta N=0.05$ and a simulation box of size $L_{x}\times L_{y}=5792\times 2896\lambda _{D}^{2}$ ($k_{x}$, $k_{y}$ and $\lambda _{D}$ are the parallel and perpendicular wavenumbers and the Debye length, respectively). The spectra are shown attimes $\omega _{p}t=145$, $680$, $940$, $1485$, $2020$, and $3100$. A green circle of radius $k\lambda _{D}\simeq k_{th}\lambda _{D}$ is superposed to the spectra at the first and last times ($k_{th}$ is the theoretical value). The same colorbar holds for all plots. All variables are normalized. (from Krafft and Savoini, 2022)
Fig. 1 shows, at different times, the distributions of the magnetic energy density of waves emitted at $\omega _{k} \simeq \omega _{p}$, for $\Delta N=0.05$. Electromagnetic emissions already appear at early times before Langmuir wave saturation (occurring near $\omega _{p}t \simeq 1000$), revealing a circularly distributed wave excitation pattern roughly scattered within the spectral region $ 0.004 \lesssim k \lambda _{D} \lesssim 0.01$.
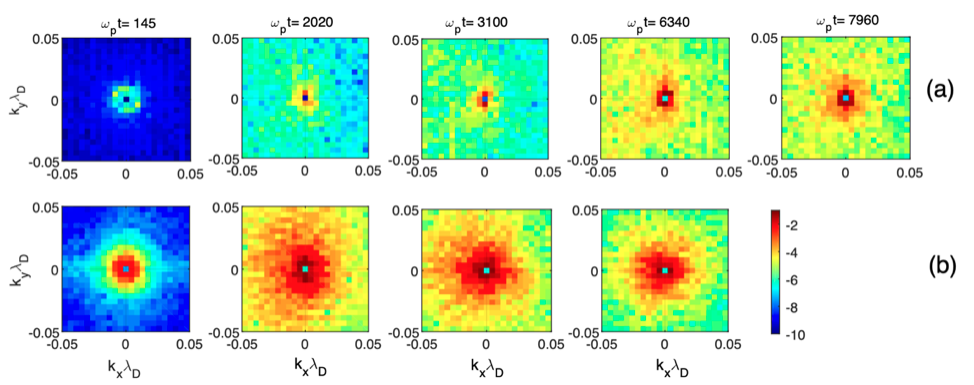
Figure 2 – Distributions of the magnetic wave spectral energy densities log$_{10}(|B_{zk}(k_{x},k_{y})|^{2})$ emitted at the frequency $\omega _{p}$, for (a) $\Delta N=0\ $(upper row) and (b) $\Delta N=0.05$ (bottom row). A box with size $ L_{x} \times L_{y}=1448 \times 1448 \lambda _{D}^{2}$ is used. The spectra are given at times $\omega _{p}t=145$, $2020$, $3100$, $6430$, and $7960$. The same colorbar holds for all plots. All variables are normalized. (from Krafft and Savoini, 2022)
Figs. 2a-b show the magnetic energy spectra $|B_{zk}|^{2}$ obtained at similar times and parameters, for $\Delta N=0$ (Fig. 2a) and $\Delta N=0.05$ (Fig. 2b), in a smaller simulation box than Fig. 1. Comparing Figs. 2a and 1-2b reveals clearly the strong impact of density fluctuations on the intensity and the spectral distribution of the electromagnetic emissions at $\omega _{p}$. In particular, at early times, the magnetic energy density is several orders of magnitude larger for $\Delta N=0.05$ than for $\Delta N=0$. In the latter case however, $|B_{zk}|^{2}$ grows continuously with time, presenting a quasi-circular shape of average radius $k\lambda _{D}\simeq 0.005$, with maxima appearing near $(k_{x}\lambda _{D},k_{y}\lambda _{D})\simeq (0,\pm 0.005)$, in agreement with the theoretical angular distribution of the nonlinear coupling coefficient of the wave interaction processes $\mathcal{L\pm S}\rightarrow \mathcal{ F}$, which is proportional to $\sin ^{2}\theta $, where $\theta $ is the angle between the electromagnetic and the Langmuir wavevectors (e.g. Ziebell et al., 2015). Then Fig. 2a exhibits for the uniform plasma the expected dipolar radiation structure at all times, only not at $\omega _{p}t=145$ where the emission is very weak. This property is not observed in the presence of density fluctuations, as the scattering phenomena contribute to isotropize the emission patterns.
During all the beam relaxation, the amount of electromagnetic energy radiated at $\omega _{p}$ in the inhomogeneous plasma strongly exceeds that observed in the absence of density fluctuations. Nevertheless, asymptotically, the amplitudes of these emissions become roughly the same whether the plasma is homogeneous or not, due mainly to the dynamics of Langmuir wave turbulence during its saturation stage and of the beam. Note that, for $\Delta N=0.05$, the fraction of Langmuir wave energy involved in the generation of electromagnetic emissions at $\omega _{p}$ saturates around $10^{-4}$, i.e. one order of magnitude above that reached when the plasma is homogeneous.
Finally, the joint time evolution of electromagnetic waves radiated at fundamental $\omega _{p}$ and harmonic $2 \omega _{p}$ frequencies (see also Krafft and Savoini, 2021), in a plasma without or with density fluctuations, shows that in the homogeneous case, harmonic emission dominates over fundamental emission during all evolution whereas, when the plasma contains density fluctuations, the latter is strongly dominant during several thousands of plasma periods before to be overcome by the former when the total electromagnetic energy begins to saturate.
Based on recent paper: Krafft, C. and Savoini, P., 2022, ApJL, 924, L24. DOI: 10.3847/2041-8213/ac46a7
References
Reid, H.A.S. and Ratcliffe, H., 2014, Res. Astron. Astrophys., 14(7), 773.
Celnikier, L.~M., Harvey, C.~C., Jegou, R., Moricet, P., and Kemp M., 1983, A&A, 126, 293.
Krupar, V., Maksimovic, M., Kontar, E. P., et al., 2018, ApJ, 857, 82.
Ziebell, L.F., Yoon, P.H., Petruzzellis, L.T., Gaelzer, R., and Pavan J., 2015, ApJ, 806, 237.
Krafft, C. and Savoini, P., 2021, ApJL, 917:L23.
Krafft, C. and Savoini, P., 2022, ApJL, 924, L24.