Shocks and type II bursts
Radio type II bursts are observed in association with flares and coronal mass ejections (CMEs). Metric type II bursts can be observed in dynamic radio spectra as slowly drifting emission lanes, with drift rates approximately 0.1 — 1.0 MHz/s. The start frequency of metric type II bursts is usually at about 100 — 200 MHz. The mechanism behind the bursts is generally assumed to be a propagating shock which creates electron beams that excite Langmuir waves, which in turn convert into radio waves at the local plasma frequency and its harmonics.
The exact relationship between solar flares, shocks, and coronal mass ejections is still not well understood, and it is of interest to know how shocks are initiated and under which conditions radio type II bursts can be excited. As shocks can be formed in various ways, it is not evident that all solar radio type II bursts are formed in the same way. In particular, how are untypical, fragmented type II bursts that start at very high frequencies, created? Are there differences in shock acceleration or in the surrounding medium that can explain the differences to the “typical” metric type IIs?
The 13 May 2001 radio event
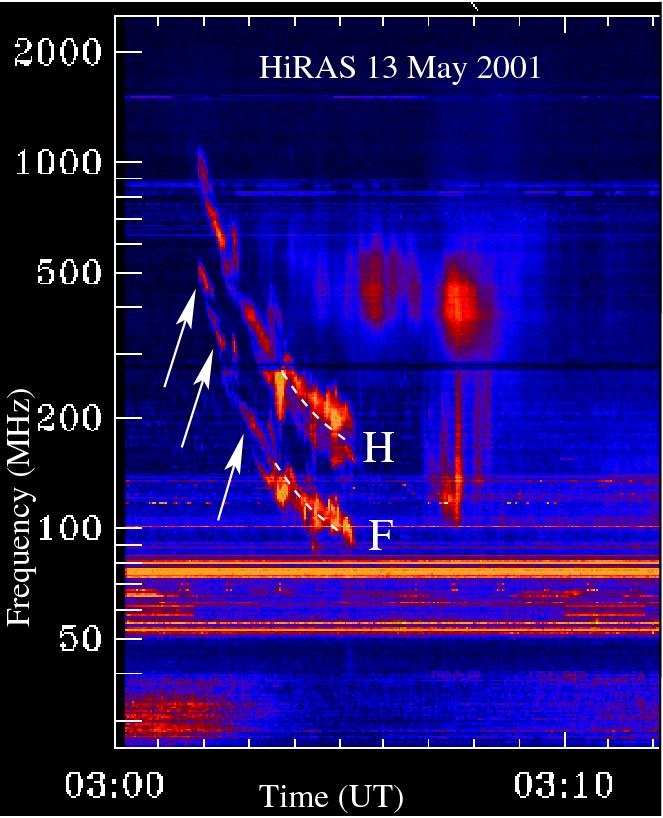
We have analysed in detail one metric type II burst that occurred on 13 May 2001. It was observed at the Hiraiso Solar Observatory (NICT), in Japan. The burst started at an unusually high frequency and proceeded showing fragmented and curved emission bands, which were visible at the fundamental and second harmonic plasma frequencies. ‘F’ in the spectral plot marks emission at the fundamental and ‘H’ at the second harmonic plasma frequency. Arrows point to the fragmented emission bands and dashed white lines outline the later-appearing regular type II burst lanes. The first “fragment” showed emission between 500 and 420 MHz, which correspond to densities in the range of 2 — 3 ×109 cm-3. The second fragment near 03:02 UT gives densities 1 — 2 × 109 cm-3 (400 — 310 MHz), and the third near 03:03 UT gives densities 2 — 6 × 108 cm-3 (220 — 130 MHz). These values indicate that the source regions were dense, similar to active region loops. Rough estimates for heliocentric heights, using atmospheric density models up to ten-times Saito (Saito, 1970), give values in the range of 1.03 — 1.43 R⊙. These estimates are suggestive, since the models do not give heights for erupting structures.
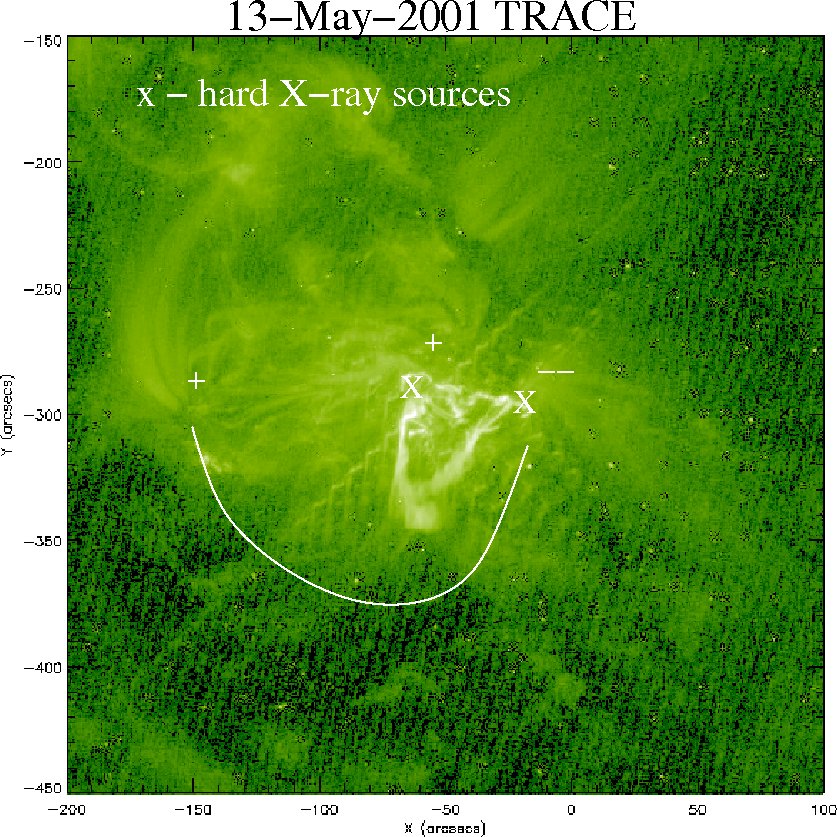
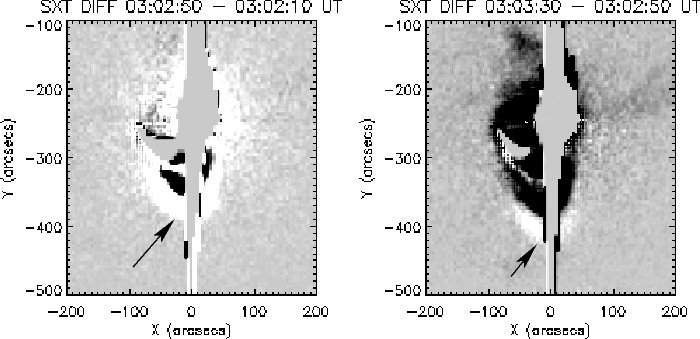
The flare was well-observed in X-rays (Yohkoh) and EUV (TRACE). The images show a filament eruption, where most of the material is moving toward the Southeast. The outermost front of the filament moves with a projected speed of about 380 km/s, but there is also a separate ‘blob’ that moves more to the Southwest with a projected speed of 450 km/s (below, on the left). A soft X-ray loop system is observed moving southward at a projected speed of about 650 km/s (difference images below, on the right). Using the Yohkoh SXT filter ratio method (see, for example, McTiernan et al., 1993), we found that the soft X-ray loop densities agreed with the plasma densities of the fragmented metric type II burst. White-light observations from SOHO LASCO also revealed a CME front moving toward the South at a speed of 430 km/s.
 |
 |
MHD simulations
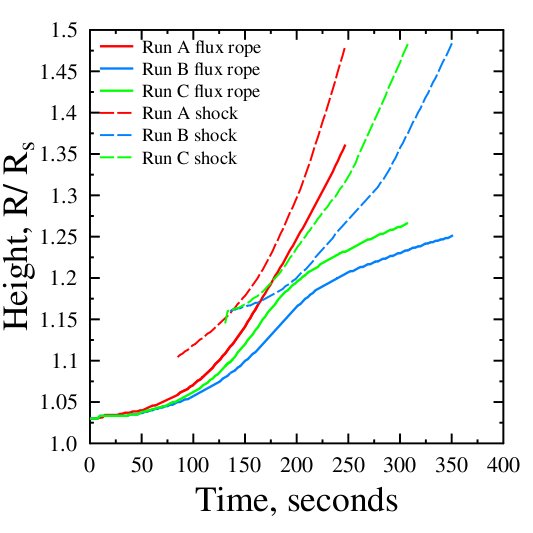
We then utilized numerical MHD simulations to study the shock structure induced by a CME, in a model corona including dense loops. The details of the model are presented in Pomoell, Vainio, and Kissman (2008). We plot below, on the left, the height-time profile of the filament and the shock. We consider three different runs with slightly different parameters. The plot on the right shows the radio emission produced by a shock, assuming that the emission is produced immediately in front of the CME leading edge shock. The emission lanes show a frequency drop in accordance with the exponentially decreasing density of the ambient corona. However, when the radio-emitting shock propagates in a dense loop, the frequency is higher, and drops quickly when the shock exits the loop (near t = 200 seconds). Additionally, we indicate the compression ratio of the shock by the size of the marker. In all three cases, the shock is strong while it propagates in the loop, with the compression ratio remaining between 3 and 3.5.
 |
 |
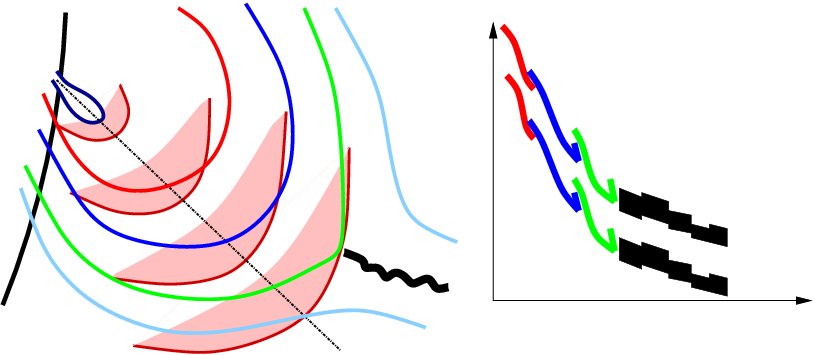
The dynamics of the eruption is as follows: As the flux rope starts to rise, a perturbation is formed around the flux rope. Due to the gradient in the Alfven speed and the increasing speed of the flux rope, the wave steepens to a shock ahead of the flux rope. However, the strength of the shock remains weak in the area below the loop. When the shock reaches the dense loop, it strengthens and slows down quickly due to the low Alfven speed in the loop. The erupting filament continues to push the loop structure ahead of it, acting as the driver of the shock. Thus, the speed of the shock is roughly that of the displaced loop structure when propagating in the region of low Alfven speed. As the filament decelerates, the displaced loop and shock escape from the filament. When reaching the region of higher Alfven speed, the speed of the shock increases with the increasing Alfven speed, and the shock escapes from the propagating loop structure. A possible scenario for a fragmented type II burst can be the following (see schematic model below): An erupting filament drives a strong shock wave through a system of overlying loops. Among these loops, a few are more favorable sites for plasma emission than others, e.g., because of their higher density or suprathermal electron content. These loops are “lit” in radio as the shock traverses them, producing the fragmented part of the radio burst. The regular part of the burst may then come from the part of the active region above the loop system, e.g., from an overlying current sheet. (See, e.g., Mancuso and Abbo 2004, for a similar geometric model involving the interaction of a shock and a current sheet.) Finally, the burst dies out or even stops abruptly once the shock propagates out of the region completely.
 |
More details on this event and the numerical simulations are available as a preprint (ADS entry), and the paper will be published soon in Astronomy & Astrophysics.
References:
Mancuso, S., and Abbo, L. 2004, Astron. Astrophys. 415, L17; McTiernan, J.M., Kane, S.R., Loran, J.M., et al. 1993, Astrophys. J., 416, L91; Pomoell, J., Vainio, R., & Kissmann, R. 2008, Solar Phys., in press; Saito, K. 1970, Ann. Tokyo Astr. Obs., 12, 53
