Solar radio emission is produced in the turbulent medium of the solar atmosphere, and its observed properties (source position, size, time profile, polarization, etc.) are significantly affected by the propagation of the radio waves from the emitter to the observer. Scattering of radio waves on random density irregularities has long been recognized as an important process for the interpretation of radio source sizes (e.g., Steinberg et al. 1971), positions (e.g., Fokker 1965; Stewart 1972), directivity (e.g., Thejappa et al. 2007; Bonnin et al. 2008; Reiner et al. 2009), and intensity-time profiles (e.g., Krupar et al. 2018, Bian et al. 2019). While a number of Monte Carlo simulations have been developed to describe radio-wave scattering (mostly for isotropic density fluctuations), not all agree.  The present work addresses this important issue both by extending and improving the previous descriptions.

Methodology & Results

In the recent paper, we reviewed the numerical Monte Carlo technique used to solve the Langevin equations modelling both source sizes and time profiles.  Isotropic scattering is inconsistent with observations of solar radio source sizes and time profiles.  Therefore, we constructed a new model that allows quantitative analysis of radio-wave propagation in a medium that contains an axially symmetric, but anisotropic, scattering component.  Explicit expressions for the Langevin equations in the case of anisotropic scattering were derived and presented in section 3.2 of Kontar et al. (2019).

The properties of the sources, as obtained from the ray-tracing simulations (see Figure 1), were studied assuming the photons propagated in different angles to the line-of-sight (LOS) of the observer (see Figure 2).  We found that the FWHM source size along the x-direction decreases with increasing angle from the LOS, whereas the FWHM source size in the y-direction changes only weakly.  The observed sources are found to be circular at $\theta = 0$ (with respect to the LOS), but the observed sources become more elliptical as $\theta$ becomes larger (Figure 2).  Interestingly, although the radio-wave scattering effects lead to large source sizes, the directivity is predominantly in the radial direction; an outcome that differs from early results suggesting isotropic directivity (emission pattern) due to scattering.

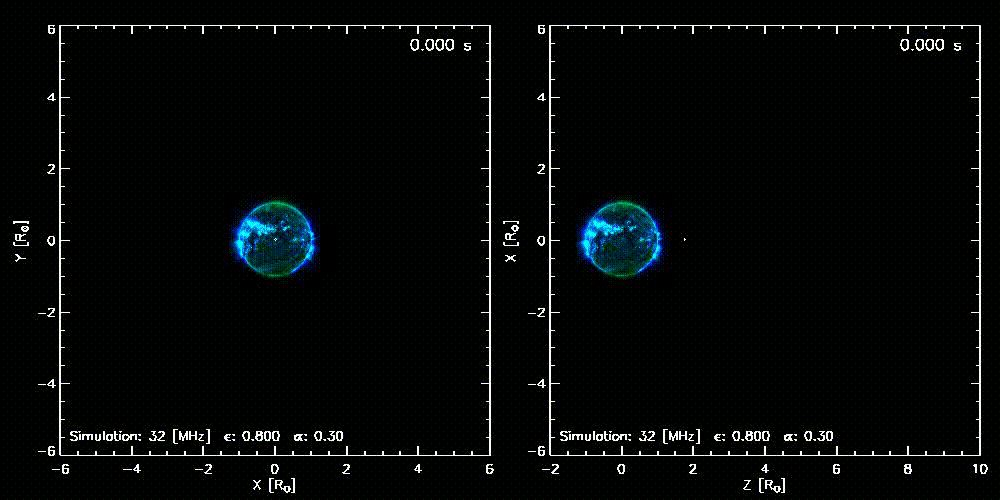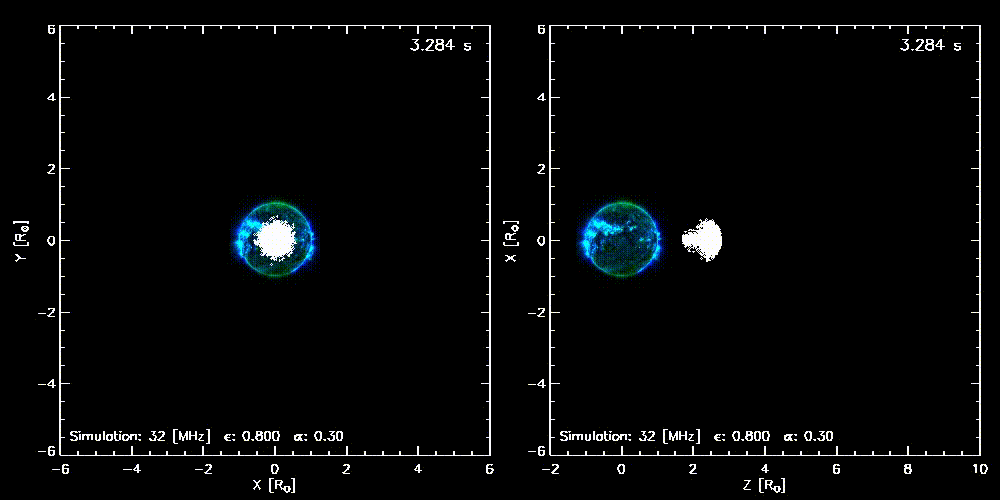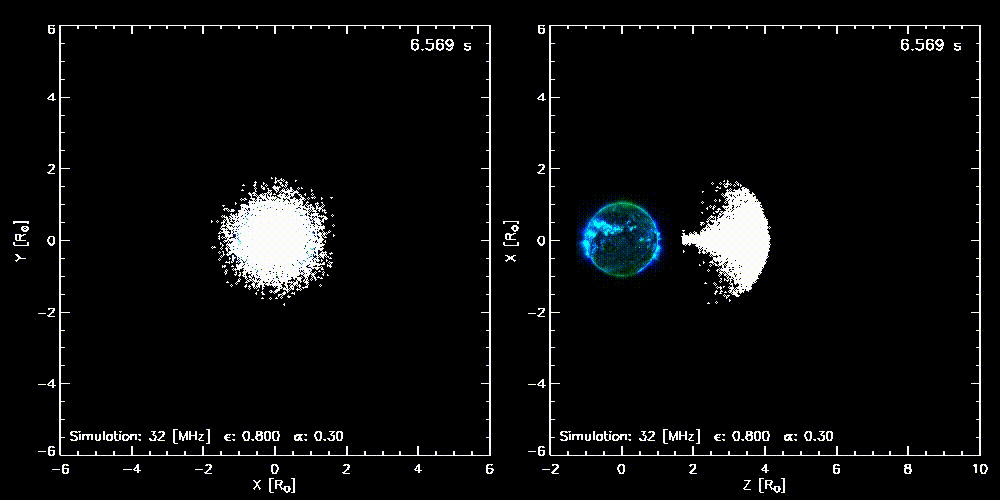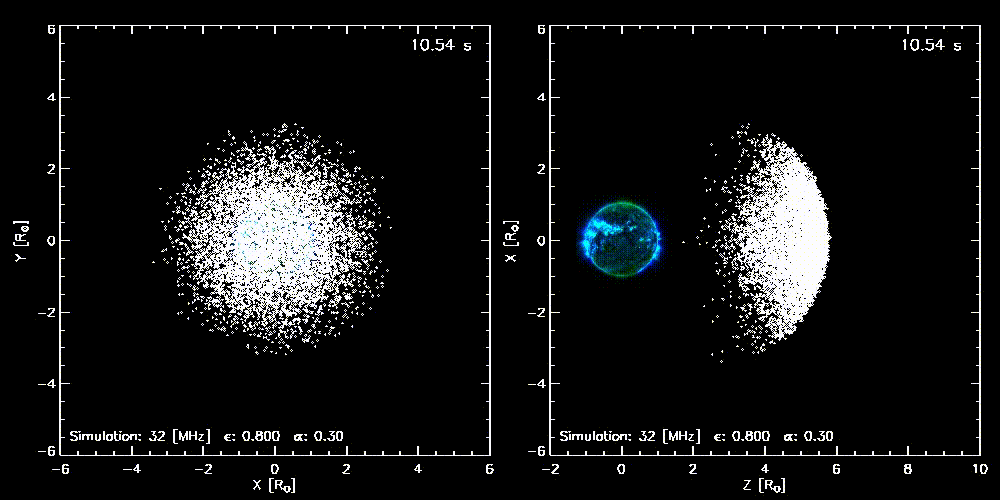
Figure 1.  An animation showing how photons from a radio point source emitting at 32 MHz are affected by radio-wave propagation effects as they travel into the heliosphere (where $\alpha = 0.3$ and $\epsilon = 0.8$).  The left panel illustrates the way the source will appear if it propagates directly towards the observer, whereas the right panel indicates how the source will appear if it propagates perpendicular to the line-of-sight of the observer.  (Figure adapted from Kontar et al. (2019).)

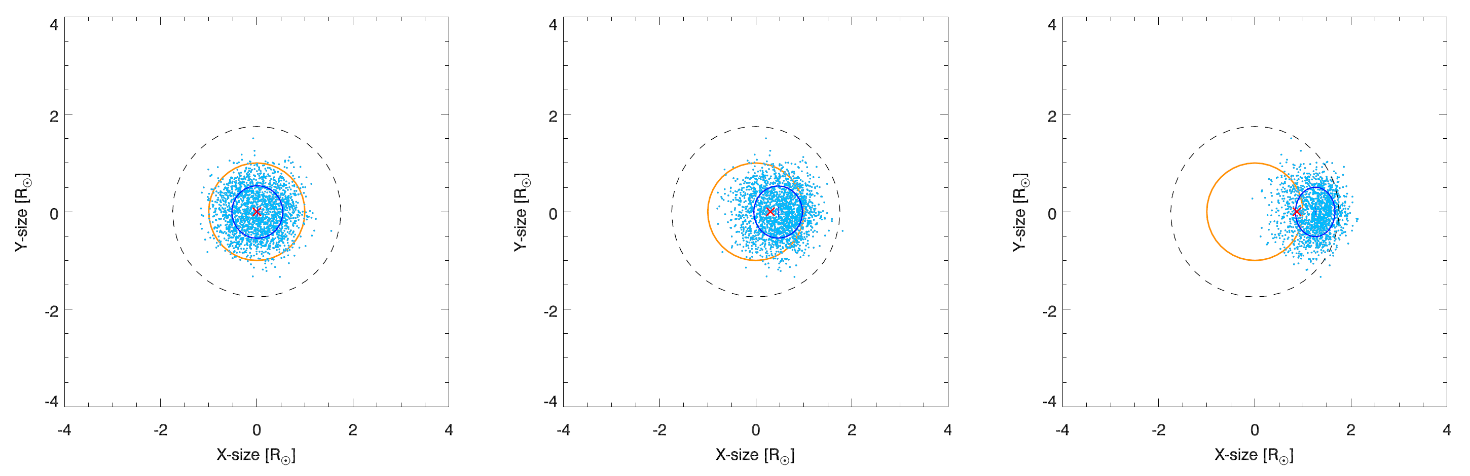
Figure 2.  Simulations of a source affected by radio-wave propagation effects as it travels at different angles to the observer’s line-of-sight.  The left, middle, and right panels illustrate the appearance of a source propagating at angles $\theta = 0^o, 10^o, 30^o$, respectively, to the line-of-sight of the observer.  The photos (light blue dots) are emitted from a point source (red cross) at 32 MHz ($1.75 R_\odot$, indicated by the grey, dashed line) and propagate through a medium with a turbulence level $\epsilon = 0.8$ and anisotropy $\alpha = 0.3$.  The apparent position and FWHM size of the source, with respect to the Sun (orange circle), are indicated in a dark blue cross and circle, respectively.  (Figure adapted from Kontar et al. (2019).)

Source size and time profile measurements from the numerical Monte Carlo simulations were compared to observations of source sizes and decay times over a wide range of frequencies ($\sim 0.02 – 500$ MHz).  We found that both the source size and decay time of the observations can be matched only if anisotropy is taken into account, whilst when ignored, only one of the two properties can be matched at a time.

Conclusions

The main result of our work comes from the comparison of the simulations with the combined imaging and time-delay observations as a function of frequency.  Such comparison leads us to the conclusion that observations of Type III solar radio burst sizes and durations, over a broad range of frequencies, require anisotropic scattering in the entire heliosphere between the Sun and the Earth, with an anisotropy factor $\alpha \approx 0.3$ and with the density fluctuations predominantly perpendicular to the radial direction.  At the same time, conclusions regarding the level of density fluctuations $\epsilon$ are also dependent on, and so require knowledge of, the outer density scales $l_0(r)$.  For example, to explain the observations near 30 MHz, a high level of density fluctuations $\epsilon = 0.8$ is required for the adopted model of $l_0(r)$. The numerical model developed suggests that anisotropic density fluctuations (lower power in the parallel direction) are required to account for the source sizes and decay times simultaneously, for all types of radio bursts emitting plasma radio emission.

Based on the recent publication by Eduard P. Kontar, Xingyao Chen, Nicolina Chrysaphi, Natasha L.S. Jeffrey, A. Gordon Emslie, Vratislav Krupar, Milan Maksimovic, Mykola Gordovskyy, Philippa K. Browning, Anisotropic Radio-wave Scattering and the Interpretation of Solar Radio Emission Observations, The Astrophysical Journal, 884 122 (2019) DOI: 10.3847/1538-4357/ab40bb

Additional info

The Monte Carlo routine (“ray_new.pro”) for 3D anisotropic scattering simulations has been publicly shared and is accessible through the  SolarSoftWare (SSW) library at NASA or via Glasgow University link. The installation is discussed at LOFAR ISSI Team webpage.

References
Arzner, K., & Magun, A. 1999, A&A, 351, 1165
Bian, N. H., Emslie, A. G., & Kontar, E. P. 2019, ApJ, 873, 33
Bonnin, X., Hoang, S., & Maksimovic, M. 2008, A&A, 489, 419
Fokker, A. D. 1965, BAN, 18, 111
Krupar, V., Maksimovic, M., Kontar, E. P., et al. 2018, ApJ, 857, 82
Reiner, M. J., Goetz, K., Fainberg, J., et al. 2009, SoPh, 259, 255
Steinberg, J. L., Aubier-Giraud, M., Leblanc, Y., & Boischot, A. 1971, A&A, 10, 362
Stewart, R. T. 1972, Proc. Astron. Soc. Aust., 2, 100
Thejappa, G., & MacDowall, R. J. 2008, ApJ, 676, 1338
Thejappa, G., MacDowall, R. J., & Kaiser, M. L. 2007, ApJ, 671, 894