


Next: 2.5.3 Debugging
Up: 2.5 Code topics
Previous: 2.5.1 Profiling
[ID index][Keyword index]
Just say no! Or, if you need authority:
[ Donald Knuth, in Literate
Programming ]Premature optimization
is the root of all evil.
The first thing to ask yourself, when you are considering
performance enhancements on your code is `do I really need
to do this?'. You should only attempt optimizations once
you have either identified a particular part of your code
which needs improving, or else you know that you
can write the efficient version of the code correctly. If
the `efficient' version is unnatural, then the savings in
runtime you achieve by reordering the code have a good
chance of being wiped out by the time spent debugging a
convoluted juggling act. Within reason, prefer simplicity
and robustness to efficiency[Note 8] -- get
your code working correctly and believably, and only then
start worrying about speed. That way, if you later
establish that you need to work on part of the code, you
at least have a trusted set of results to check the new
version's against. Another way of putting this is that
it's easier to optimize correct code than it is to correct
optimized code.
If you're writing a code which will run for days or more,
then it might be worthwhile investing a significant effort
in tuning your code for performance. Doing this properly
might involve you learning more about your machine's
architecture than you might enjoy, and as as result will
make your program less portable to the next generation of
whizz-bang hardware, or even the next compiler.
It is generally worthwhile to use hand-optimized
routines, if they are available for your compiler. Where
this can pay particularly good dividends is in the case of
linear algebra, where the speed of a calculation can be
significantly improved (`a factor of several') by routines
carefully written to access memory in an optimal way.
There is a standard interface to such routines called the
BLAS (Basic Linear Algebra Subroutines), which your
compiler documentation may mention. Although it won't
be as fast as a machine-specific implementation, the free
BLAS
implementation at Netlib (UK
mirror) should speed your codes up
significantly. [MBT,RW]
The first lesson to learn about optimization is that the
compiler can probably do it better than you can.
Most compilers will have a -On option, to
allow you to set how aggressive the compiler's
optimization will be. The GNU gcc compiler, for example,
allows optimization levels 1, 2 and 3, and Solaris Fortran
has five levels, which progressively enable more
techniques for improving your program's execution speed.
Compaq compilers have a `-tune host' option,
to produce code optimized for a particular machine. [MBT]
If your program starts behaving oddly, at some point you
should start worrying about errant optimization, if you
have that turned on. Optimization works by the compiler
recognising patterns in your code, and possibly
rearranging the output assembly language to take advantage
of these. If it gets this wrong (because there's a bug),
if your program relies on a particular floating-point
behaviour, or if you're doing something sufficiently weird
with your programming language that you manage to confuse
the compiler, then you could trick it into doing the wrong
thing.
Specifically, if you have occasion to worry about the
order in which expressions are evaluated -- for example to
conserve precision, as described in Section 2.3.2.2
-- then you should be very wary of optimization, as one of
the first things an optimizer might do is to
reorder expressions which are associative mathematically
but not computationally. If you have some code like this,
it might be best to isolate a single routine in a module
of its own and compile it separately with its own
appropriate optimization level.
Parallelization is another type of optimization. Just
say no several times to this, but if you have an
application which really needs it, then buy a book and
some aspirins. See Section 2.5.2.7.
Although you should generally leave optimization to the
compiler, there are some things you can do to at least
avoid getting in its way.
This is, historically, supposed to suggest to a
compiler that a particular variable might be better
stored in a register than in main memory, though the
actual semantics defined in the C standard is that the
keyword is an assertion that the program nowhere takes
the address of the variable so qualified. Such an
assertion means, amongst other things, that the variable
will never be visible from any other functions, which
might trigger other optimizations. [SG]
You do not need to use this keyword to actually suggest
to the compiler that it store the variable in a
register, since the compiler might well do this anyway,
and have a better idea of which (non-obvious, or
temporary) variables to choose than you have.
A multi-dimensional array is necessarily stored in
memory as a linear array. If you have to process this
entire array, it will be fastest if you try to do so in
the order in which the array is stored. Fortran arrays
are stored with the leftmost index varying fastest.
That is, the Fortran array integer i(2,2)
will be stored in memory in the order
i(1,1), i(2,1),
i(1,2) and i(2,2)
Take,
for example the Fortran array integer
ia(1000,1000). If you run through this array
with the first index changing fastest, as in the
following fragment
do 10,
j=1,1000 do 20, i=1,1000 call some_calc (ia(i,j)) 20
continue 10 continue
then
you will move through the array in the `natural' order.
If, however, you process it in the other order, with the
second index changing fastest, then when you move from
ia(i,j) to ia(i,j+1), the
computer will have to jump 1000 places forward in the
stored array, each time round the loop. This would not
matter too much if the entire array were stored
in physical memory, but this will not be the case for
any sizable matrix, so that to find the appropriate
array element, the machine may have to reload part of
its memory from a saved version on disk. Such input is
relatively slow, and if the calculation is laid out in
such a way that this happens repeatedly in an inner
loop, which is executed many times by an outer loop,
then there can be a significant impact on your program's
performance.This system of swapping memory back
and forth to disk is known as `virtual memory', and the
machine's discovery that the memory it needs is swapped
out is known as a `page fault', and is one of the
important statistics about the run of your program. You
can obtain such statistics in copious detail by using
the compiler's profiler (see Section 2.5.1),
or quickly by using the time command (see
your system's time man-page for details --
not all versions provide this information by default).
Of course, it's not really as simple as just
that. Even when the entire array is stored in
physical memory, or when you have rearranged your
program to minimise the number of page faults, it can be
important not to hop about in arrays too much. Modern
architectures will typically have a small amount (modern
PCs around half a Mb, biggish servers around 8 Mb) of
memory called `cache' which has much faster access time
(typically an order of magnitude or more) than the bulk
of the RAM. The relationship between this and core RAM
is strongly analogous to the relationship between core
RAM and disk, in that cache-lines (which are like memory
pages, but typically only a few words long) get swapped
in and out of it when one word from the line is
required. The upshot of that is that it's important to
avoid hopping about over distances much smaller than an
I/O page since, even if you have no page faults, cache
faults make a huge difference. And of course it's not
as simple as that either -- sometimes there are two
levels of cache, some architectures implement some sort
of prefetching, and so on. Except with some rather
sophisticated profilers (which generally have to be
supported by a processor architecture which keeps a
record of these things) it's not really possible to see
how many cache faults you're getting, except by writing
the code more efficiently and seeing what the difference
is. [MBT]
Unlike Fortran,
C arrays are stored with the rightmost index
increasing fastest, so that the array int
i[2][2] will be stored as i[0][0],
i[0][1], i[1][0] and
i[1][1].
Input and output are slow, and the faster processors become, the
bigger is the cost of I/O relative to CPU cycles. That means you
should think twice before writing out intermediate results, for reuse
later in the same calculation or another. For example, it's quite
easy to fall into the trap of `saving time' by reading in a
precalculated table of values, without realising that it can take more
time to read the file than it would take to recalculate the table from
scratch each time. Remember that computers don't get bored, and don't
mind doing the same calculation repeatedly.
If you do need to save values for later use, and don't
mind doing it only semi-portably, you can save time and
precision by using raw I/O rather than formatted ASCII
[RW].
A C example is:
FILE *ofile; float arr[10];
/* set arr[i] to have sensible values */
ofile = fopen ("output-c.dat", "w");
fwrite ((void*)arr, sizeof(arr[0]), 10, ofile);
fclose (ofile);
Note that we carefully cast the variable
arr to type void*, and that we
could replace this by (void*)&arr[0] if
we thought it was clearer. Note also the minor trick of
using sizeof(arr[0]) rather than the more
obvious sizeof(float); they are equivalent,
but the first will remain correct even if we change our
mind about the size of the elements of the array
arr. You would read the contents of this
file in using the function fread.The fwrite and fread
functions are not portable in general, since they deal
with floating point numbers merely as bundles of bits,
and pays no attention to how these are interpreted.
This means that such files are not portable between
machines which interpret these bits differently, so that
files written on a little-endian machine (see Section 2.3.2) will be gibberish if read on a big-endian
machine, and vice-versa. However, C's raw I/O is
semi-portable, inasmuch as the
fwrite function above does nothing other
than copy 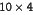 bytes
(in this case) from memory to disk;
bytes
(in this case) from memory to disk; fread
similarly copies bytes from disk to memory without any
interpretation.
The corresponding Fortran example is
real arr(10)
C set arr() to have sensible values
open (unit=99,file='output-f.dat',form='unformatted')
write (99) arr
close (99)
Note that Fortran unformatted output is not portable in
any way. Unlike C raw I/O, the Fortran compiler is free
to store the information on disk in any way it likes,
and the resulting file will not, in general, have 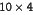 bytes in it. That
is Fortran unformatted I/O is machine- and
compiler- specific, and the file
bytes in it. That
is Fortran unformatted I/O is machine- and
compiler- specific, and the file
output-f.dat in this example will only be
readable in general using a Fortran program built using
the same compiler.As described in Section 2.3.2.3, any operation
which has a NaN as input, produces a
NaN as its result. Similarly, the special
values positive and negative Infinity are
legitimate numbers which can appear in a calculation.
Consider the following code fragment:
do 10, i=-5000,5000
do 20, j=-5000,5000
if (j .ne. 0) then
t(i,j) = real(i)/real(j)
else
t(i,j) = 0.0
endif
20 continue
10 continue
The if test is to avoid a division-by-zero
error. If this loop were buried deep within a hierarchy
of other loops, then the test could be the source of a
significant fraction of the runtime. It can, however be
omitted, allowing the matrix t(i,j) to
include numerous Infinitys and one
NaN (due to 0/0). Because both of these
values are permissable floating-point operands, they can
be allowed to percolate through the rest of the
calculation without elaborate further tests, to be
checked only at the end. This is possible only if the
floating-point environment is set up not to
generate signals on floating-point exceptions (see also
Section 2.3.2.3).Note that calculations involving the exceptional values
tend to run more slowly than those using normal values,
so if your calculation produces a significant number of
exceptional values -- like the artificial example above
-- a switch to IEEE semantics might not produce a speed
win overall. Note also that the expression
(a.lt.b) is not equivalent to
.not.(a.gt.b), since both
a.lt.b and a.gt.b are false
when one of the variables is an IEEE exceptional value:
this could produce hard-to-find bugs if you were not
alert to this when you were writing the code. [SG]
It may or may not be obvious that debugging and
profiling options, as discussed in Section 2.5.3 and Section 2.5.1, will
both slow your program down (especially in the latter
case), and make it bigger. You should compile your
program, or at least the numerically intensive parts of
it, without them when you are not debugging it. [MBT]
Random points:
- This is a case where free software is not
necessarily better. Both Sun and Compaq expend
resources on making their compilers as efficient
as possible. If speed is important to your
application, you're probably best off using one of
these compilers.
- On the Alpha, it's worth while using the
Fortran 90 compiler even for Fortran 77 code [SG].
Take a look at the Sun Numerical Computation Guide
[sunncg], particularly the end of
chapter 5, and at the collection of papers at
<http://sunsite.doc.ic.ac.uk/sun/Papers/SunPerfOv+references/>,
particularly the helpful paper about compiler switches:
you_and_your_compiler (this is a generally
useful collection of Sun papers, by the way).
If you do need to spend significant effort
tuning your code, then you should consult a textbook on
the matter. A good one is High Performance
Computing [dowd]. This
reference touches on parallelizing your code, a topic
which I have deemed sufficiently arcane not to be
discussed at all in this introductory guide.



Next: 2.5.3 Debugging
Up: 2.5 Code topics
Previous: 2.5.1 Profiling
[ID index][Keyword index]
Theory and Modelling Resources Cookbook
Starlink Cookbook 13
Norman Gray
2 December 2001. Release 2-5. Last updated 10 March 2003