Astronomy 2, Relativity and Gravitation (2023–24)

Lecture 1, 2023 September 20, 11:00Introductory remarks and definitionsThis is a rather mixed lecture, where we introduce a number of definitions which will probably make more sense when you come back to reexamine them later. (mp3, transcripts: html, txt, vtt).

Lecture 2, 2023 September 21, 11:00Understanding the axiomsStating, and working through the implications of, the two axioms of SR (mp3, transcripts: html, txt, vtt).

Lecture 3, 2023 September 28, 11:00Length contraction, and the light-clockWe start looking at the direct implications of the SR axioms, and discover the phenomena of time dilation and length contraction in qualitative terms. Considering then the thought-experiment of the light-clock, we are then able to obtain a quantitative expression for time dilation. (mp3, transcripts: html, txt, vtt).

Lecture 4, 2023 October 04, 11:00Introducing the Minkowski diagramFirst of all, we learn about 'natural units', which seem perplexing, but which are just, at base, a sensible choice of time unit. Then we go on to develop the 'Minkowski diagram', which we will see _much_ more of in the weeks to come. (mp3, transcripts: html, txt, vtt).

Lecture 5, 2023 October 05, 11:00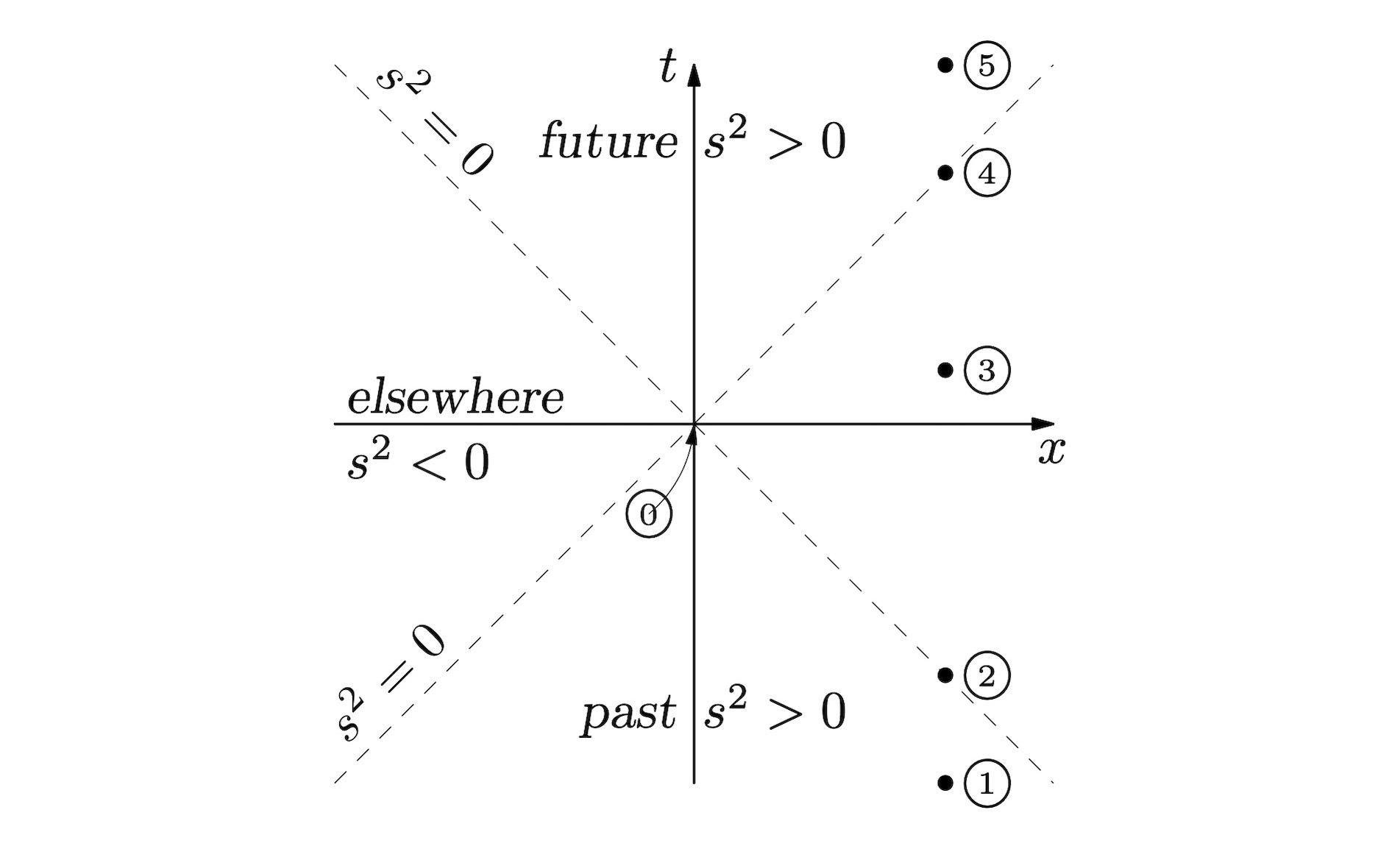Stressing geometryIn which I have a lot more to say about geometry, and the notion of the frame-invariant squared-interval. (mp3, transcripts: html, txt, vtt).

Lecture 6, 2023 October 11, 11:00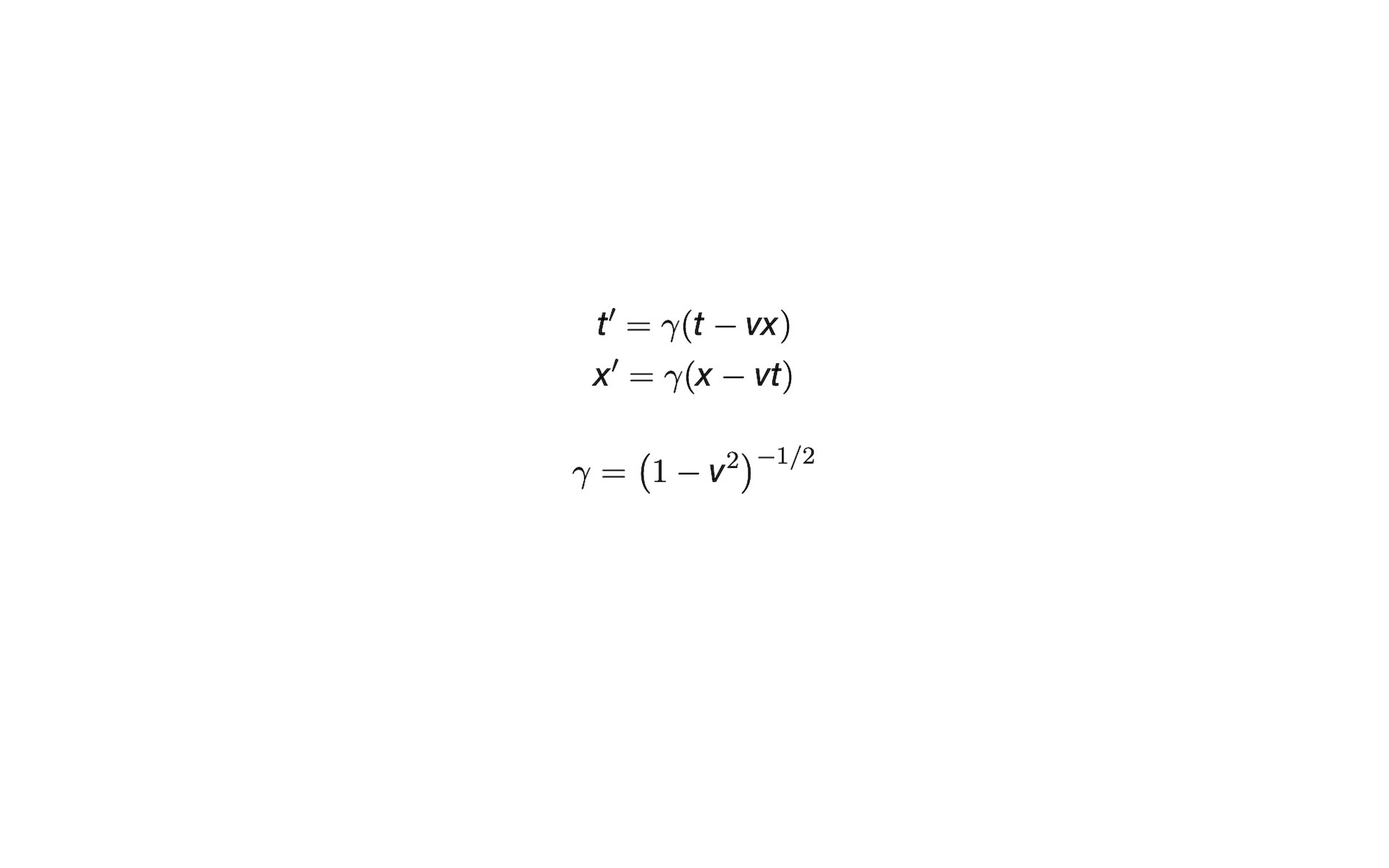The Lorentz TransformationThis is one of a few different ways of introducing the Lorentz Transformation. This version emphasises the role of geometry in SR, by _starting_ from the frame-invariance of the squared-interval, and proceeding from there. I mention the ‘recipe’ – I'll have lots more to say about that in the weeks to come. (mp3, transcripts: html, txt, vtt).

Lecture 7, 2023 October 18, 11:00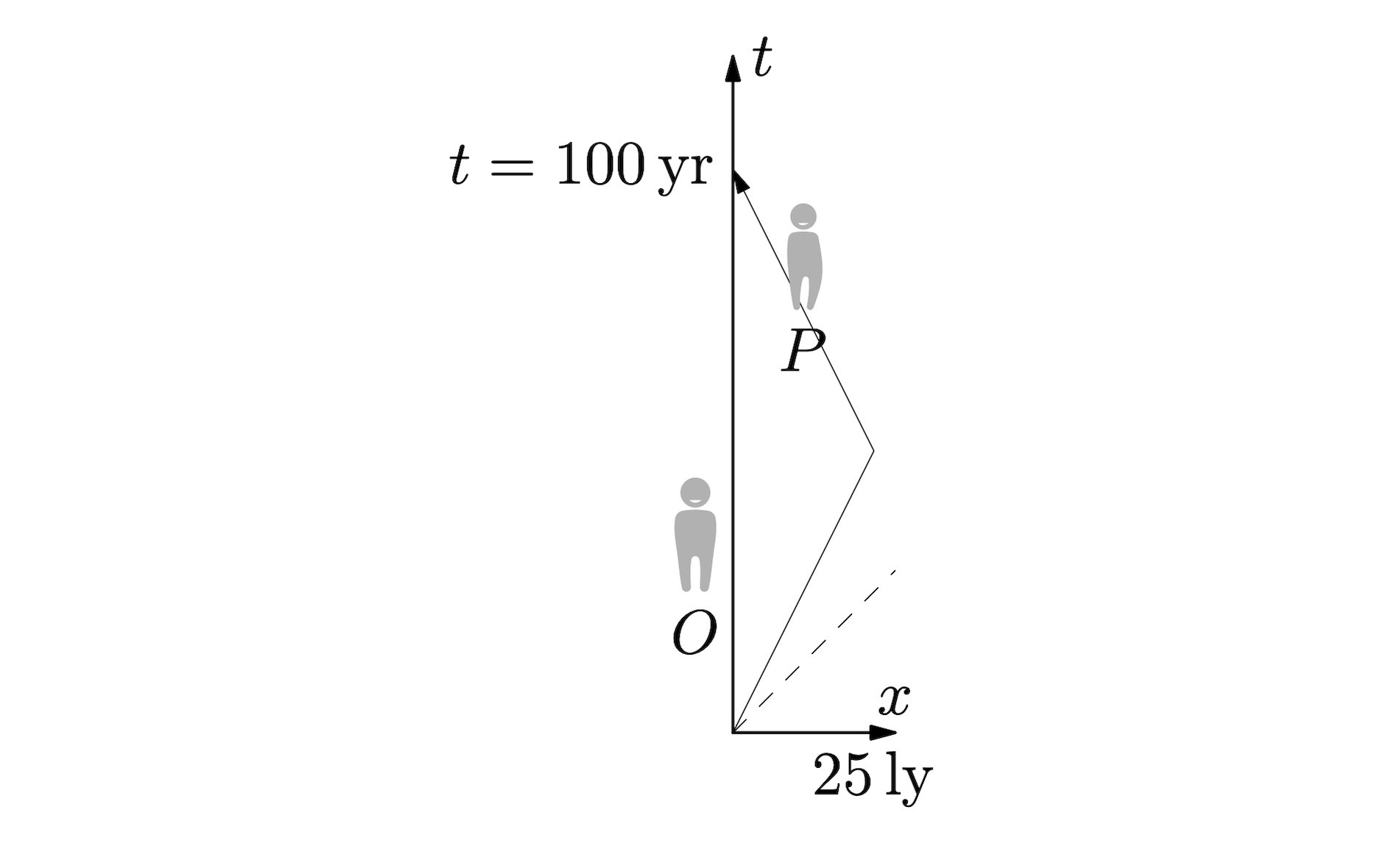ParadoxesA ‘paradox’, in this context, is an argument – typically a thought-experiment of some type – which appears to lead to an inconsistent or nonsensical conclusion, but which turns out to be consistent (and typically illuminating) on closer examination. In this lecture, we look at three such ‘paradoxes’. (mp3, transcripts: html, txt, vtt).

Lecture 8, 2023 October 19, 11:00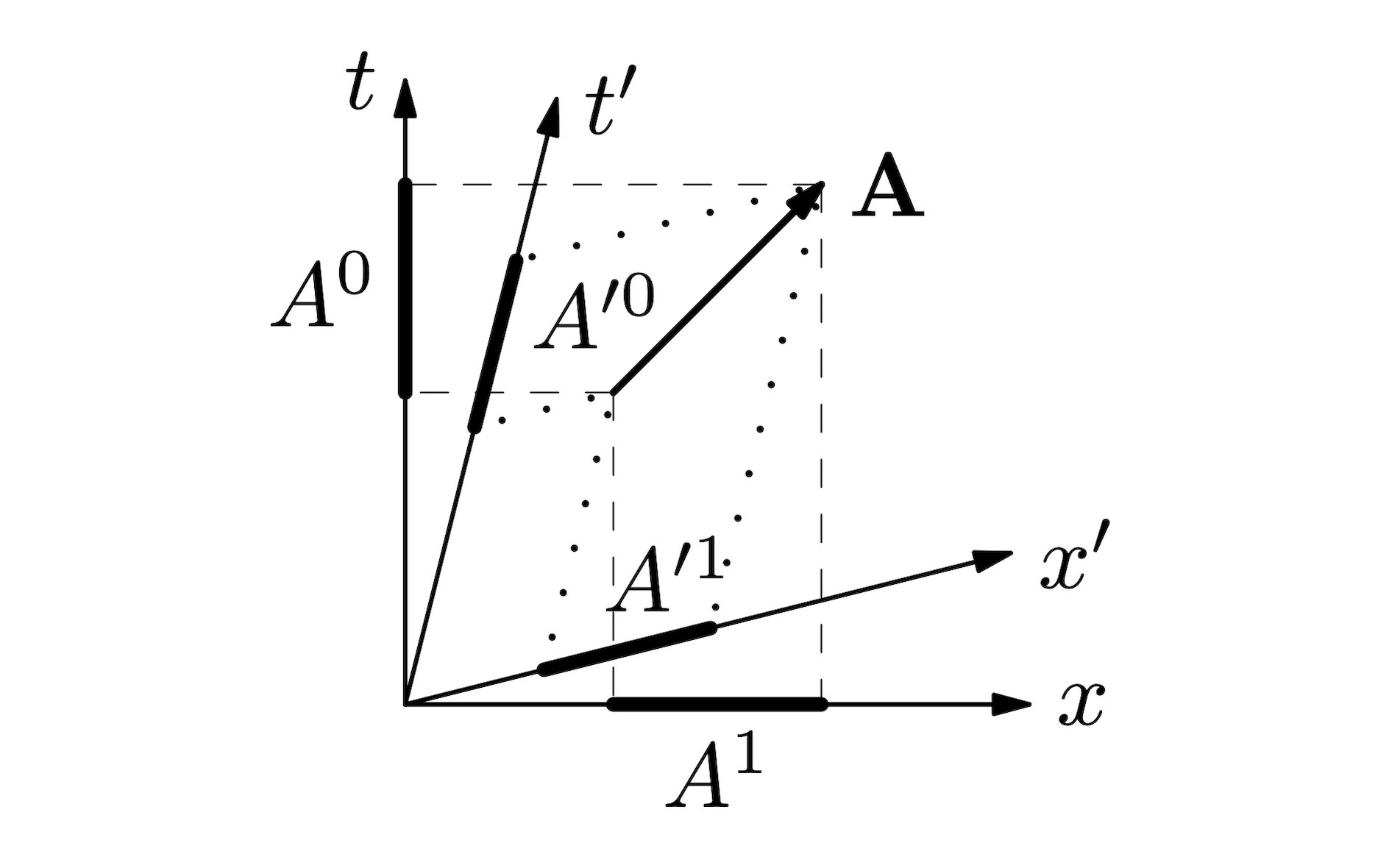Kinematics, and 4-vectors in Minkowski spaceIn order to explain motion, we must first be able to describe it. First, we learn about 4-vectors, and how they are the same as, and how they are different from, the 3-vectors we're used to. The first 4-vector we examine is the velocity 4-vector, and we define it, and look at some of its properties. (mp3, transcripts: html, txt, vtt).

Lecture 9, 2023 October 24, 11:00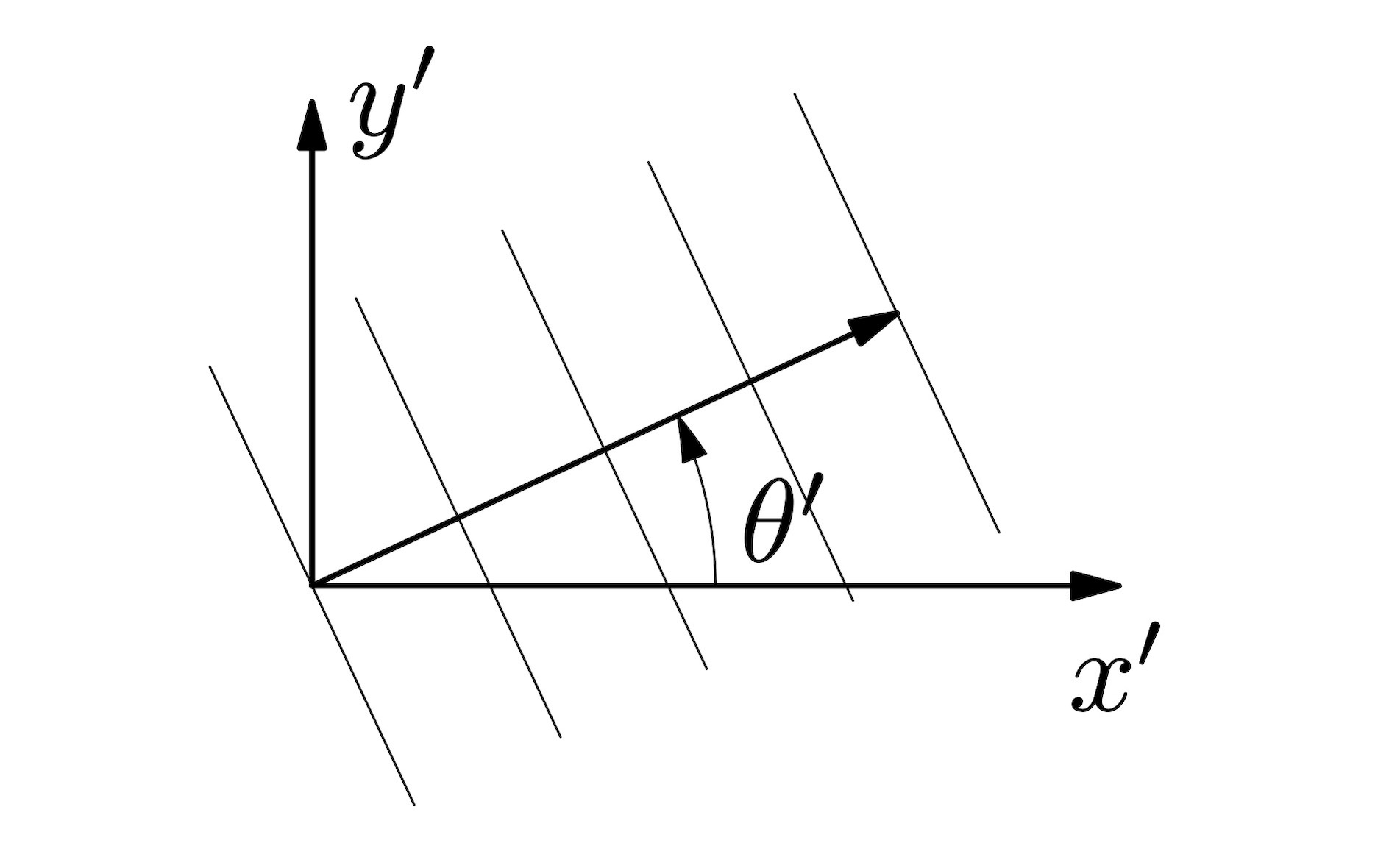The frequency vector and the Doppler shiftWe have discussed 4-vectors in general, and the velocity and acceleration 4-vectors in particular. Now it's time to define and examine a further one, the _frequency_ 4-vector. If we define this the correct way, then we can use the properties of 4-vectors, in their transformation from frame to frame, to learn how to describe the frequency and direction of a (light) wave, in different frames. We end up with a compact derivation of the relativistic doppler shift. (mp3, transcripts: html, txt, vtt).

Lecture 10, 2023 October 25, 11:00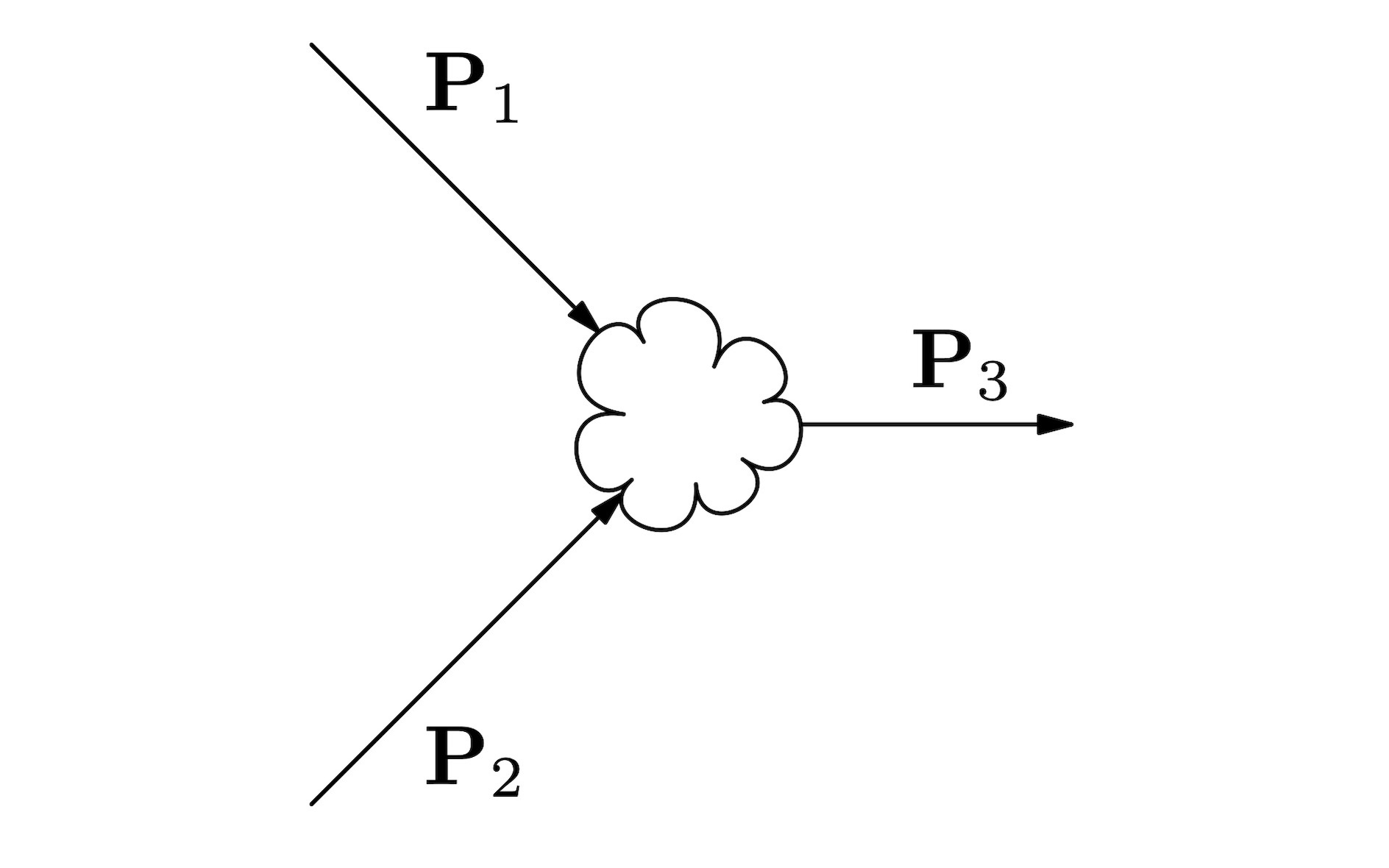Dynamics, and the momentum -vectorKinematics is the description of motion; dynamics is the explanation of motion. After a brief worked example, on the use of the freqency 4-vector, we go on to define the momentum 4-vector, in a straightforward way based on the velocity 4-vector. We discover that it's reasonable to regard the 4-momentum as being conserved in collisions, component by component. When we apply this to the zeroth- or time-component of the momentum, we discover that this corresponds, in a slightly indirect way, to the _energy_ of a particle, and we discover, moreover, that the energy of a particle is non-zero even when the particle is at rest: E=mc^2. (mp3, transcripts: html, txt, vtt).

Lecture 11, 2023 November 01, 11:00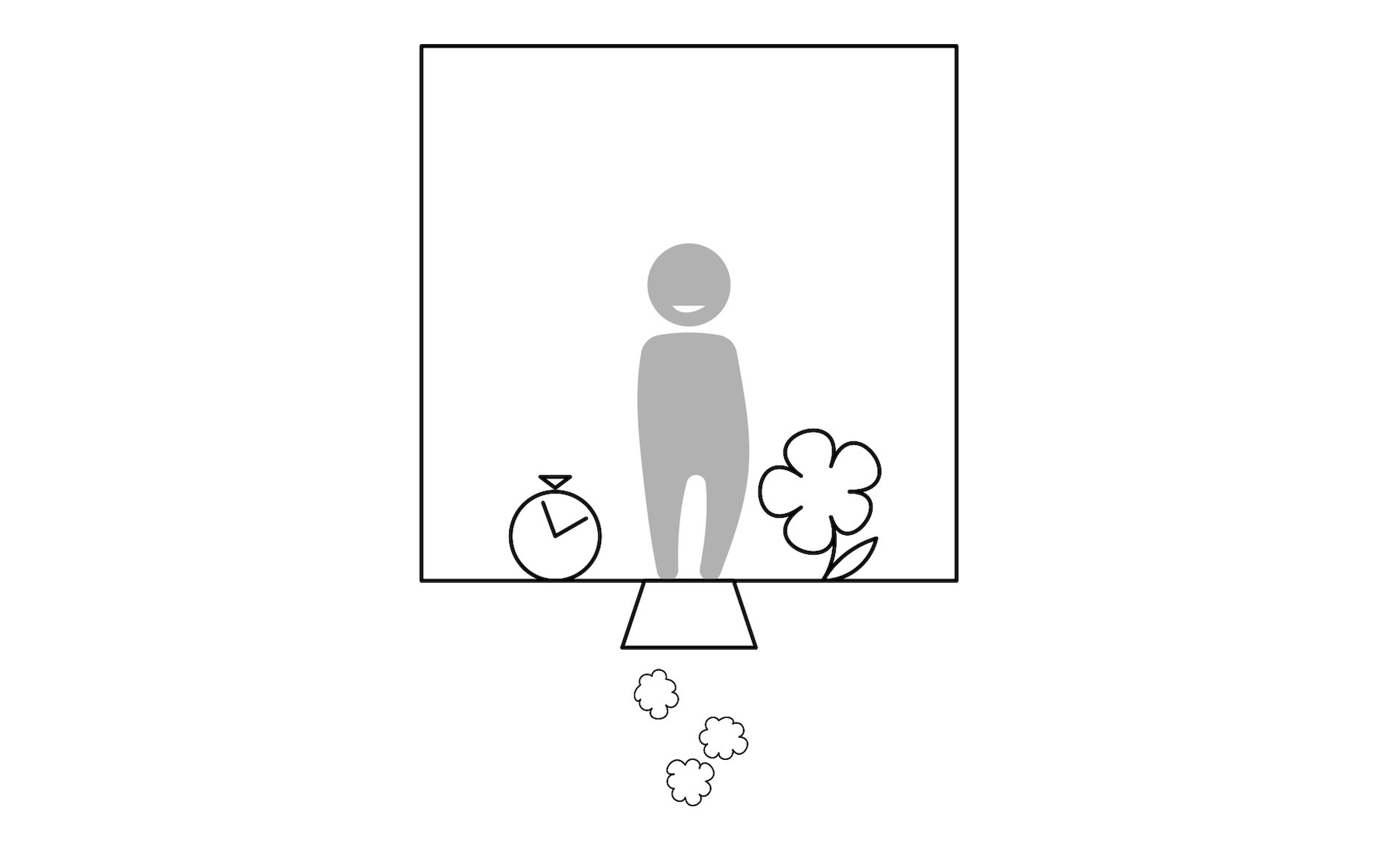An introduction to the ideas of General RelativityHaving _Done_ SR – Special Relativity, or the special case of non-accelerating frames – we can now look at the general case. We need to talk about gravity, and the way we do that is by starting off with the case of _no_ gravity, namely a box floating in space. What can we deduce about how physics works in that box, and what connections can we make between the physics we see when that box is accelerated by a rocket, and what we see when that box is sitting on the Earth? We can suppose that these two situations are more closely linked than we might at first thing, and make that link through the Equivalence Principle. (mp3, transcripts: html, txt, vtt).

Lecture 12, 2023 November 08, 11:00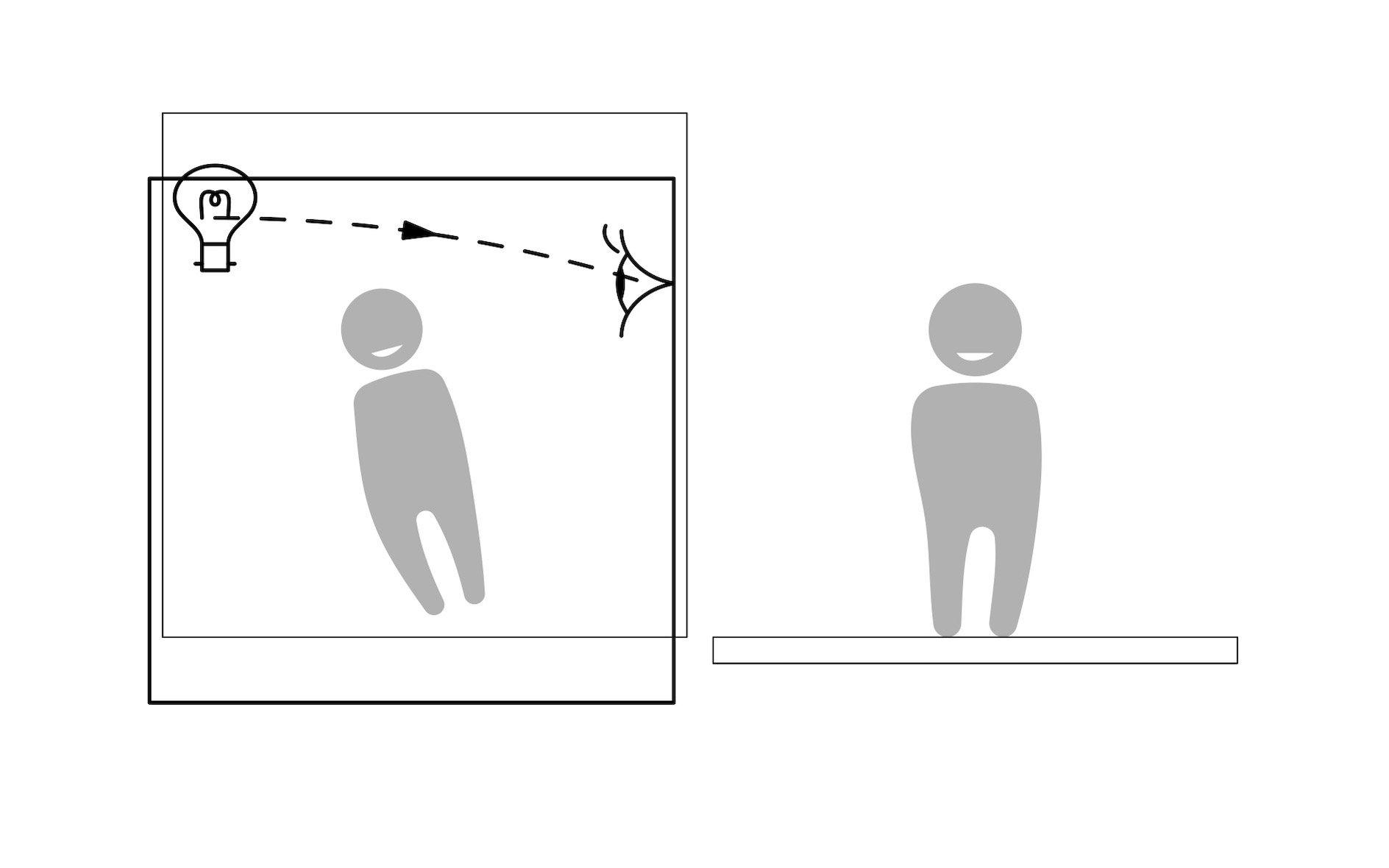More thought-experiments: EP, bending light, redshift, and the metricWe briefly discussed one version of the Equivalence Principle (EP) last time, but we now look at a second and stronger version of the EP, and at the immediate consequence of that that promptly tells us that light must bend in a gravitational field. We similarly promptly discover that light must be redshifted in a gravitational field, and are even able to calculate by how much. We go on to take a second look at the ‘invariant interval’ that we looked at in previous weeks, and discover that that was the first view of the _metric_ that is central to General Relativity (GR). (mp3, transcripts: html, txt, vtt).

Lecture 13, 2023 November 14, 11:00An introduction to general relativity: geometry, metrics, curvature and geodesicsWe can characterise the geometry of a space by its _metric_. Metrics range from the very simple (pythagoras's theorem is essentially a statement of the metric for euclidean space), to the semi-familiar (you already have some experience of the different geometry of the surface of the celestial sphere) to the more exotic (the invariant interval of Special Relativity is really a _metric_ for Minkowski space). Added to this we can talk of a _geodesic_ as the generalisation of a ‘straight line’ in an arbitrary space. The final ingredient is a further version of the Equivalence Principle, which allows us to link what we know about Special Relativity, which works in a flat inertial frame, to motion in a curved spacetime. The result is one half of the key notions of General Relativity, that ‘space tells matter how to move’. (mp3, transcripts: html, txt, vtt).

A2 R&G lecture-tutorial, 2023 November 15, 11:00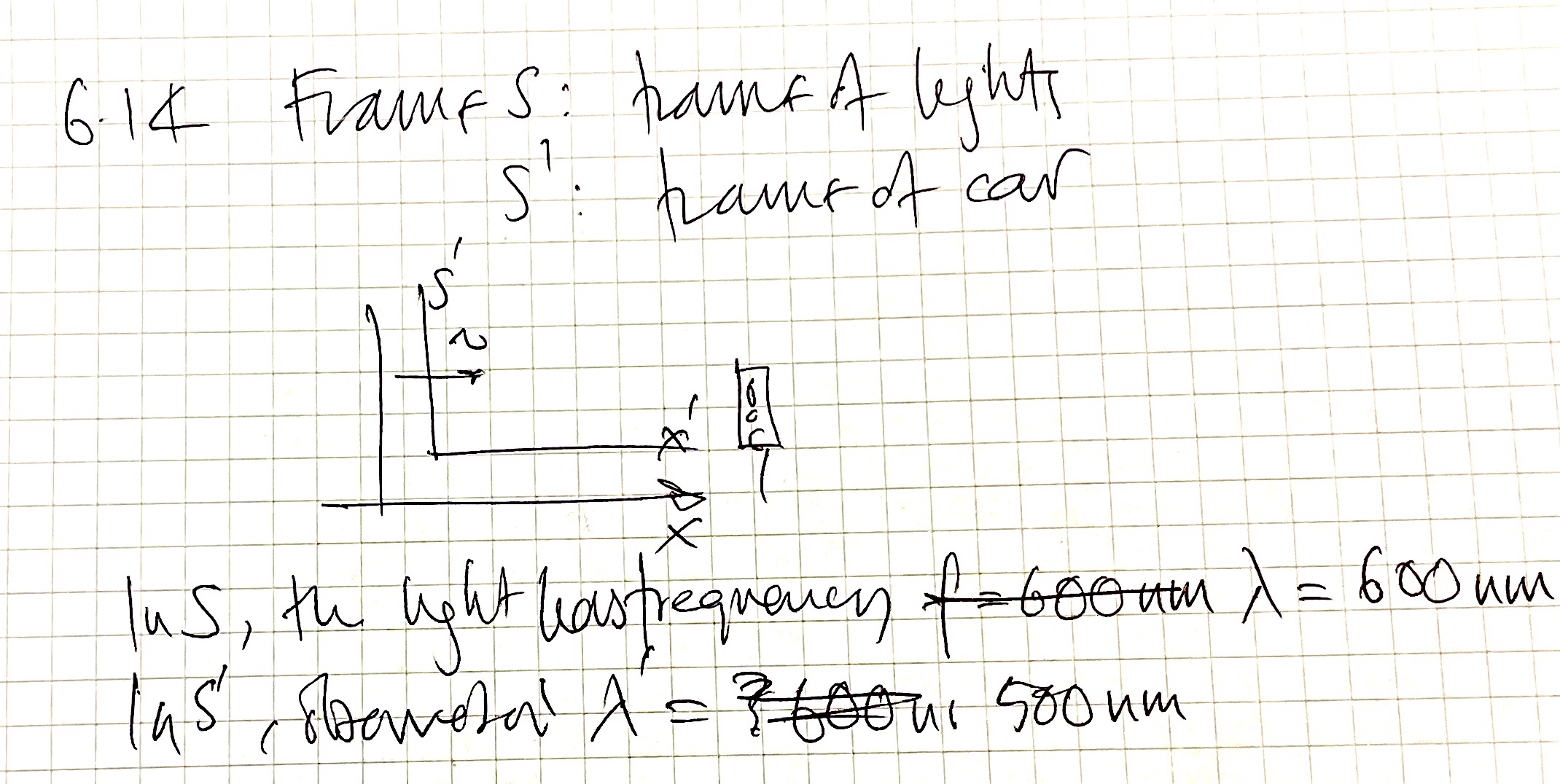Two worked examplesI work through exercises 4.7 and 6.14, talking about the SR in question, but also making a number of remarks about assessment and exam strategy. (mp3, transcripts: html, txt, vtt).

Lecture 14, 2023 November 16, 11:00An introduction to the key solutions of Einstein's equationAfter finishing off a last few remarks from ch,8, we now look at various solutions to Einstein's equations, which are possible in special cases. We cover the ‘weak field’ approximation, for ‘small’ masses moving non-relativistically, and learn that this regenerates Newton's law for universal gravitation. We look at the case of a single isolated mass, and at the Schwarzschild solution in this case. (mp3, transcripts: html, txt, vtt).

Lecture 15, 2023 November 22, 11:00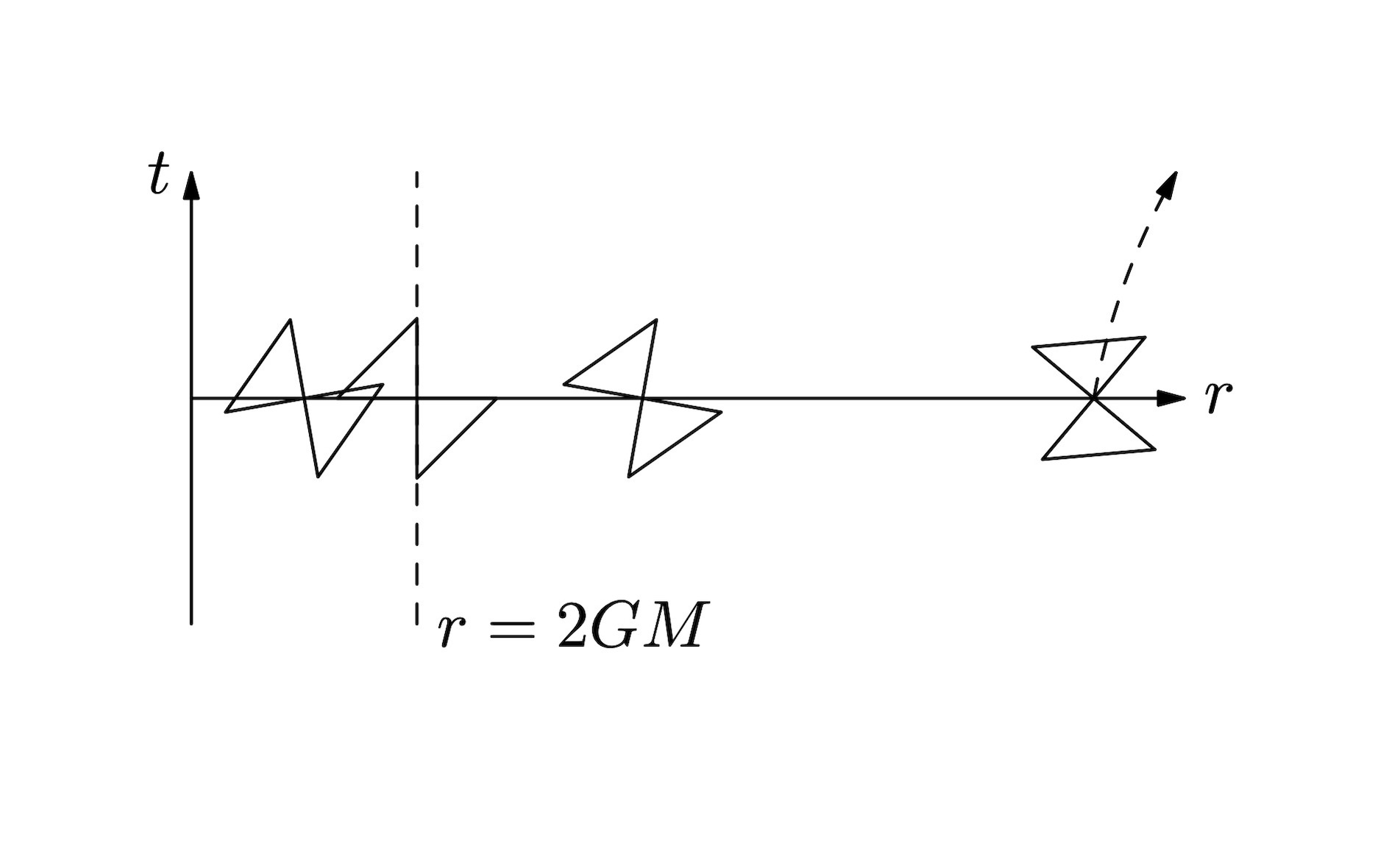The Schwarzschild metric, black holes, gravitational waves, and cosmologyIn this final lecture, we look at some of the consequences of the Schwarzschild metric, in particular their prediction of the event horizon of a black hole. We look briefly at what a gravitational wave is, and the key observations which confirm their existence. And we look briefly at the FLRW solution for the spacetime of the universe as a whole. (mp3, transcripts: html, txt, vtt).