Contents
MATLAB Basics
For more help and demos type 'doc' at the command line. This document can be found on the web at:
clear
Simple Sums
a=3
% semicolon at the end of a line supresses output
b=4;
c=a+b
a =
3
c =
7
You can do the same with arrays (matricies)
Thre is no need to loop over array indicies in MATLAB - array and matrix operations are done in the same way as scalar operations.
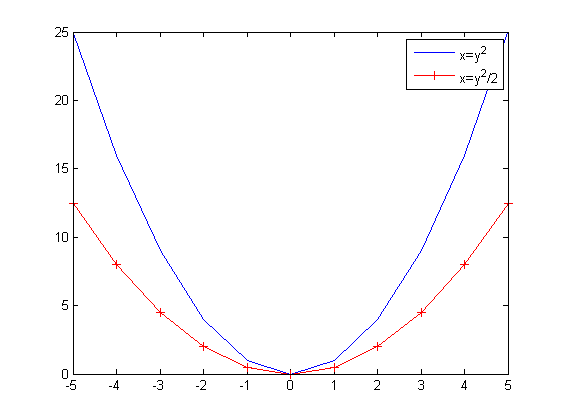
% the colon operator makes ranges x=-5:5 % to multiply arrays element by element use .*, simlilarly ./ for division and .^ for power y=x.^2 plot(x,y); %to add a second plot hold on; plot(x,y/2,'r-+'); hold off; legend('x=y^2','x=y^2/2'); % to get simple help at the command line: % help plot % for more detailed help % doc plot
x =
-5 -4 -3 -2 -1 0 1 2 3 4 5
y =
25 16 9 4 1 0 1 4 9 16 25
matrix operations
a*b does a matrix multiplication
a=[1; 2; 3]
b=[10:12]
c=a*b
% to see what variables we have:
whos
a =
1
2
3
b =
10 11 12
c =
10 11 12
20 22 24
30 33 36
Name Size Bytes Class
a 3x1 24 double array
b 1x3 24 double array
c 3x3 72 double array
x 1x11 88 double array
y 1x11 88 double array
Grand total is 37 elements using 296 bytes
2d arrays
clear the workspace
clear % in matlab array indexing rows x columns % to make an empty array 4 rows by 6 columns a=zeros(4,6) % set a value to a different number (row 1 col 6) a(1,3)=6; %set a range a(3:4,:)=pi; % just typing a variable name displays it a
a =
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
a =
0 0 6.0000 0 0 0
0 0 0 0 0 0
3.1416 3.1416 3.1416 3.1416 3.1416 3.1416
3.1416 3.1416 3.1416 3.1416 3.1416 3.1416
Using the meshgrid command
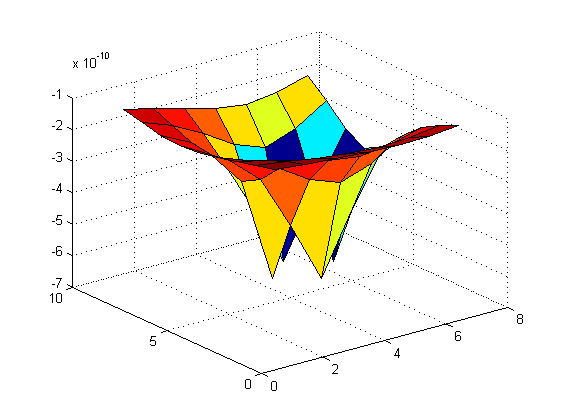
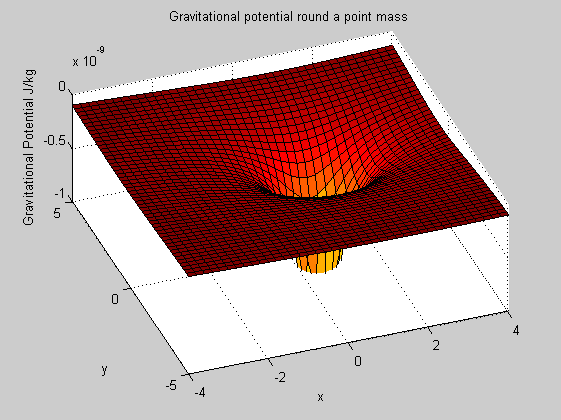
%Useful if you want to calculate a value that depends on spatial location %Example : Gravitiational potential around a point mass [x,y]=meshgrid(-3:3,-4:4) %location of mass x0=1; y0=1; m0=10; % gravitational constant G=6.67e-11; % make an array that gives the distance from the point mass to the current point r=sqrt((x-x0).^2+(y-y0).^2); U=-G*m0./r % make a surface showing the results figure(1) surf(U) % note we get a divide by zero warning, and U goes to infinity % do the same with more points to get a better looking result: xrange=-4:0.2:4; yrange=-5:0.2:5; [x,y]=meshgrid(xrange,yrange); x0=1; y0=1; m0=10; r=sqrt((x-x0).^2+(y-y0).^2); U=-G*m0./r; figure(2) surf(xrange,yrange,U); xlabel('x'); ylabel('y'); zlabel('Gravitational Potential J/kg'); title('Gravitational potential round a point mass') % set the z axis limits zlim([-1e-9 0]); view(-20,60)
x =
-3 -2 -1 0 1 2 3
-3 -2 -1 0 1 2 3
-3 -2 -1 0 1 2 3
-3 -2 -1 0 1 2 3
-3 -2 -1 0 1 2 3
-3 -2 -1 0 1 2 3
-3 -2 -1 0 1 2 3
-3 -2 -1 0 1 2 3
-3 -2 -1 0 1 2 3
y =
-4 -4 -4 -4 -4 -4 -4
-3 -3 -3 -3 -3 -3 -3
-2 -2 -2 -2 -2 -2 -2
-1 -1 -1 -1 -1 -1 -1
0 0 0 0 0 0 0
1 1 1 1 1 1 1
2 2 2 2 2 2 2
3 3 3 3 3 3 3
4 4 4 4 4 4 4
Warning: Divide by zero.
U =
1.0e-009 *
-0.1042 -0.1144 -0.1239 -0.1308 -0.1334 -0.1308 -0.1239
-0.1179 -0.1334 -0.1491 -0.1618 -0.1667 -0.1618 -0.1491
-0.1334 -0.1572 -0.1850 -0.2109 -0.2223 -0.2109 -0.1850
-0.1491 -0.1850 -0.2358 -0.2983 -0.3335 -0.2983 -0.2358
-0.1618 -0.2109 -0.2983 -0.4716 -0.6670 -0.4716 -0.2983
-0.1667 -0.2223 -0.3335 -0.6670 -Inf -0.6670 -0.3335
-0.1618 -0.2109 -0.2983 -0.4716 -0.6670 -0.4716 -0.2983
-0.1491 -0.1850 -0.2358 -0.2983 -0.3335 -0.2983 -0.2358
-0.1334 -0.1572 -0.1850 -0.2109 -0.2223 -0.2109 -0.1850
Warning: Divide by zero.