It was recently reported that a significant part of the Langmuir waveforms observed by the STEREO satellite (Graham and Cairns, 2013) during type III solar radio bursts are likely consistent with the occurrence of electrostatic decay instabilities, when a Langmuir wave \(\mathcal{L}\) resonantly interacts with another Langmuir wave \(\mathcal{L}^{\prime}\) and an ion sound wave \(\mathcal{S}^{\prime}\) through the decay channel \(\mathcal{L} \rightarrow\mathcal{L}^{\prime}+\mathcal{S}^{\prime}\). Usually such wave-wave interactions occur in regions of the solar wind where the presence of electrons beams can drive Langmuir turbulence at levels allowing waves \(\mathcal{L}\) to decay. Moreover, such solar wind plasmas can present long-wavelength randomly fluctuating density inhomogeneities or monotonic density gradients which can modify significantly the development of such resonant instabilities (Ryutov 1969; Kontar and Pecseli, 2002; Krafft et al. 2015). If some conditions are met, the waves can encounter a second decay cascade (SDC) according to \(\mathcal{L}^{\prime}\rightarrow\mathcal{L} ^{\prime\prime}+\mathcal{S}^{\prime\prime}\).
Analytical estimates and observations based on numerical simulations show that the Langmuir waves \(\mathcal{L}^{\prime\prime}\) produced by this SDC can accelerate beam particles up to velocities and kinetic energies exceeding respectively two times the beam drift velocity \(v_{b}\) and half the initial beam kinetic energy (Krafft and Volokitin, 2016). Moreover, this process can be particularly efficient if beforehand scattering effects of waves on the background plasma inhomogeneities have already accelerated a sufficient amount of beam electrons up to the velocity range where the phase velocities of the \(\mathcal{L}^{\prime\prime}\) waves are lying.
Results
The simulation results are provided by a 1D numerical code based on a Hamiltonian model (Krafft et al. 2013) which allows us to derive all the self-consistent equations governing the dynamics of the Langmuir turbulence, the beam particles and the density fluctuations \(\delta n\). The model couples modified Zakharov equations including the beam current contribution to the Newton equations governing the motion of the beam electrons. Physical parameters typical of solar wind plasmas with average levels of density fluctuations reaching up to \(\Delta n=\langle (\delta n/n_0)^2 \rangle^{1/2}=5\%\) are used (\(n_{0}\) is the plasma average density) and, in particular, of type III solar bursts and foreshock regions (e.g. Ergun et al., 1998). Initially, \(1024-2048\) waves and around \(300000\) resonant beam particles are distributed within a periodic simulation box of size \(L=10000-30000\lambda_{D}.\) Depending on the simulations, the space and time resolutions are around \(2-10\lambda_{D}\) and \(0.01-0.02\omega _{p}^{-1}\), respectively; \(\lambda_{D}\) and \(\omega_{p}\) are the electron Debye length and plasma frequency. Note that the variables used below are normalized according to \(\delta n/n_{0}\), \(\omega_{p}t\), \(k\lambda_{D}\), \(v/v_{T}\) and\(\left\vert E\right\vert ^{2}/4\pi n_{0}T_{e}\); \(E\left( z,t\right) =\sum_{k}E_{k}(t)e^{ikz}\) is the slowly varying field envelope and \(E_{k}\) is the Fourier component of \(E\); \(z\) is the space coordinate and \(k\) is the wave vector; \(T_{e}\) is the electron temperature and \(v_{T}\) the electron thermal velocity; \(n_{b}\ll n_{0}\) is the beam density.
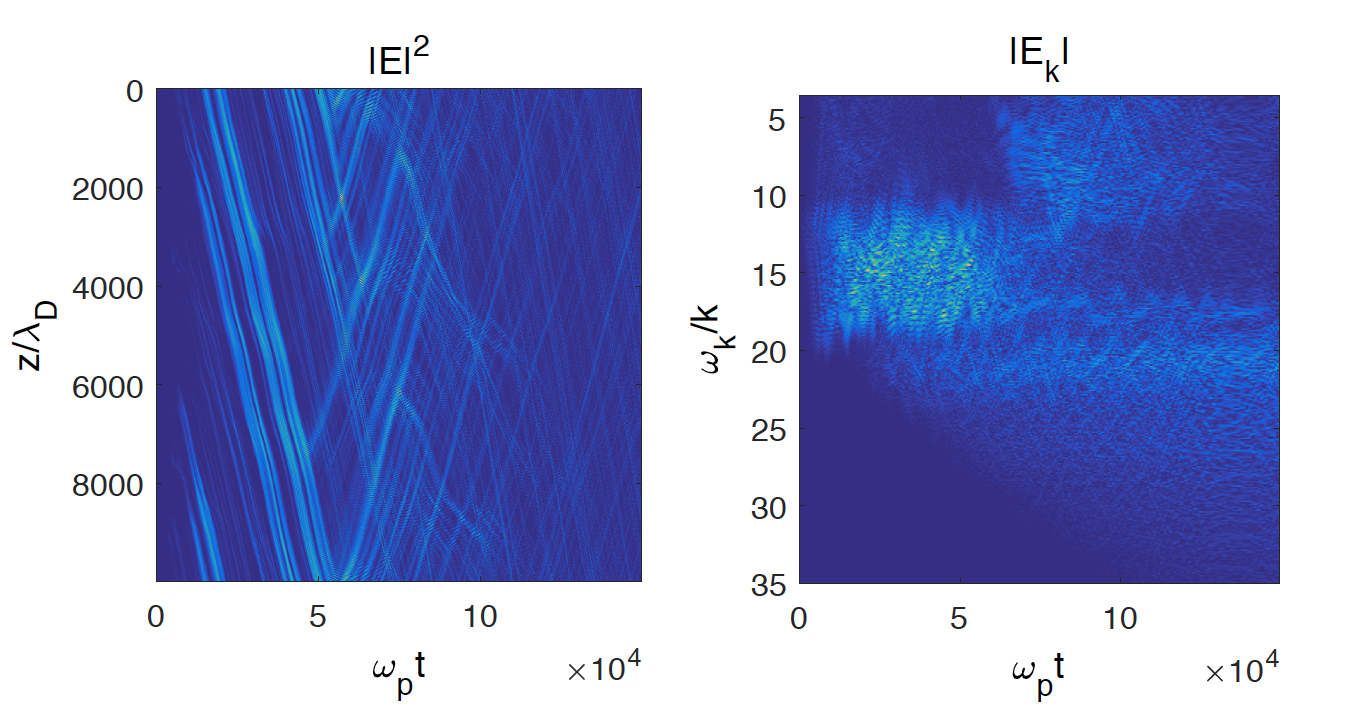Figure 1. (Left panel) Space and time variations of the normalized Langmuir energy density \(\left\vert E\right\vert ^{2}\). (Right panel) Variations with time and phase velocity \(\omega_{p}/k\) of the Fourier component \(\left\vert E_{k}\right\vert\) of the envelope of the Langmuir electric field. Main parameters are the following : \(n_{b}/n_{0}=5×10^{-5}\), \(v_{b}/v_{T}=14\), \(\Delta n\simeq0.012.\)
The evolution of the Langmuir turbulence is shown in Fig. 1, where the normalized Langmuir energy density \(\left\vert E\right\vert ^{2}\) is presented as a function of the normalized time \(\omega_{p}t\) and space coordinate \(z/\lambda_{D}\). One observes that the Langmuir packets propagate with the group velocity \(v_{g}\) until \(\omega_{p}t\simeq50000\), where the Langmuir wave decay \(\mathcal{L}\rightarrow\mathcal{L}^{\prime}+\mathcal{S}^{\prime}% \) starts (see e.g. near \(z/\lambda_{D}\simeq7500\)). Backscattered Langmuir waves \(\mathcal{L}^{\prime}\) with wavenumber \(k_{L^{\prime}}<0\) propagating with the inverse group velocity \(-v_{g}\) as well as ion acoustic waves \(\mathcal{S}^{\prime}\) with \(k_{S^{\prime}}>0\) appear as clear peaks in the corresponding spectra with expected values (not shown here). Later, near \(\omega_{p}t\simeq70000\), second cascades of the decay process, i.e. \(\mathcal{L}^{\prime}\rightarrow\mathcal{L}^{\prime\prime}+\mathcal{S}^{\prime\prime}\), occur near \(z/\lambda_{D}\simeq1500\) and \(z/\lambda _{D}\simeq6000\), producing Langmuir waves \(\mathcal{L}^{\prime\prime}\) with \(k_{L^{\prime\prime}}>0\) propagating with \(v_{g}>0\) and ion sound waves \(\mathcal{S}^{\prime\prime}\) with \(k_{S^{\prime\prime}}<0.\) The right panel of Fig. 1 shows the distribution of the Fourier component \(\vert E_{k}\vert\) along the time and the wave phase velocity \(v_{\varphi}\simeq \omega_p/k\). One observes that during a first stage the distribution is broadened around \(v_{b}=14v_{T}\) (\(v_{b}\) is the beam drift velocity), indicating that some part of the electric field intensity excited by the beam instability at \(v<v_{b}\) is transported to phase velocities higher than \(v_{b}\), as a consequence of the scattering of the beam-driven Langmuir waves on the density inhomogeneities. At later times, Langmuir energy is carried by waves with \(20v_{T}\lesssim v_{\varphi}\lesssim25v_{T}\) due to the SDC, as well as by waves with phase velocities \(u_{f}\lesssim v_{\varphi}<v_{b}\) above the beam front decelerating at speed \(u_{f}\), where the slope of \(f(v)\) remains positive during all the time evolution, even if asymptotically it tends to a quasi-plateau.
In the velocity region \(v\gtrsim v_{b}\) where the beam velocity distribution presents a negative slope during all the time evolution as well as a significant density of electrons at the time of occurrence of the SDC, the waves \(\mathcal{L}^{\prime\prime}\) which have phase velocities \(v_{\varphi }\gtrsim v_{b}\) can damp and release part of their energy to particles and accelerate them. This process can be observed in Fig. 2 (lower panel), where the part of the beam velocity distribution where \(v>v_{b}\), so-called \(f_{t}(v)\), is presented for two times after the occurrence of the first decay cascade: \(\omega_{p}t_{1}\simeq59601\) and \(\omega_{p}t_{2}\simeq126720\). At time \(t_{1}\) the scattering effects are fulfilled since at least \(40000\omega_{p}^{-1}\) whereas the first cascade of the decay process is already almost saturated; one can see that a population of accelerated particles already exists, as one of the consequences of the scattering of Langmuir waves on the density inhomogeneities, of the random shift of the wave-particle resonance condition \(kv\simeq\omega_{p}\) and of the transport of wave energy to smaller \(k\). But at time \(t_{2},\) i.e. around \(66000\omega _{p}^{-1}\) after \(t_{1}\), \(f_{t}(v)\) is significantly modified: the electron density is decreased in the range \(v_{b}\lesssim v\lesssim18v_{T}\) whereas increased for \(v\gtrsim18v_{T},\) indicating that some particles have been accelerated; this can be explained taking into account that the SDC has started near \(\omega_{p}t\simeq70000\). At times above \(t_{2}\), \(f_{t}(v)\) stabilizes and presents a monotonic decreasing negative slope: the SDC process is saturated and \(f_{t}(v)\) evolves only slightly and slowly.
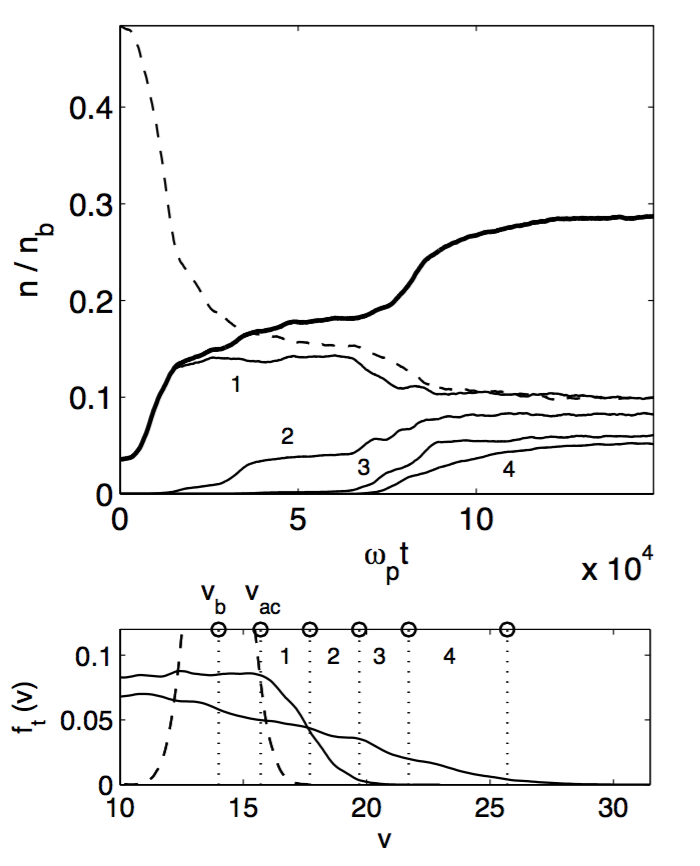
Figure. 2. (Upper panel) Time variation of the normalized densities of the accelerated beam electrons in various velocity ranges: \(n_{ac}/n_{b}=n(v>v_{ac})/n_{b}\) (upper solid line), \(n(v_{b}<v<v_{ac})/n_{b}\) (dashed line), \(n(v_{ac}<v<v_{ac}+2)/n_{b}\) (solid line 1), \(n(v_{ac}+2<v<v_{ac}% +4)/n_{b}\) (solid line 2), \(n(v_{ac}+4<v<v_{ac}+6)/n_{b}\) (solid line 3), and \(n(v_{ac}+6<v<v_{ac}+10)/n_{b}\) (solid line 4). (Lower panel): the four above mentioned ranges of velocities are shown, as well as the normalized values of \(v_{b}\) and \(v_{ac}\), the initial \(f_{t}(v)\) – in dashed lines -, and the distribution \(f_{t}(v)\) at two different times during the beam relaxation (solid lines); \(v\) is the velocity normalized by \(v_{T}\); \(v_{ac}\simeq15.7\). Parameters are the same as in Fig 1.
Let us illustrate how the normalized density \(n(v)/n_{b}\) of the beam electrons with velocities \(v\) lying within different ranges varies with time during the processes of scattering and of SDC. Fig. 2 (upper panel) shows \(n_{ac}/n_b=n(v>v_{ac})/n_b\) together with \(n(v_b<v<v_{ac})\), \(n(v_{ac}<v<v_{ac}+2)\),\(n(v_{ac}+2<v<v_{ac}+4)\), \(n(v_{ac}+4<v<v_{ac}+6)\) and \(n(v_{ac}+6<v<v_{ac}+10)\). Note that here, for simplicity purposes, \(v\) and\(v_{b}\) represent velocities normalized by \(v_{T}\). One observes that: (i) Up to the time when the scattering process is saturated (\(\omega_{p}t\simeq20000\)), the velocities of almost all accelerated particles satisfy \(v_{ac}\lesssim v\lesssim v_{ac}+2\) (region labeled by “1” in the bottom panel of Fig. 2), as they have no time to reach higher velocities; (ii) These electrons are coming mostly from the velocity range \(v_{b}\lesssim v\lesssim v_{ac}\) which also feeds the distribution of decelerated electrons; (iii) When the scattering process is saturated (\(\omega_{p}t\gtrsim20000\)), some electrons present higher velocities (see the growth of the curve 2), due to the fact that scattered waves exist with phase velocities \(v_{ac}+2\lesssim v_{\varphi}\lesssim v_{ac}+4\) (i.e.\(17.5\lesssim v\lesssim19.5,\) that is the region labeled by “2”; see also the lower panel of Fig. 1); (iv) When the second decay cascade starts (\(\omega_{p}t\simeq70000\)), the number of electrons with velocities \(v_{ac}<v<v_{ac}+2\) significantly reduces (curve 1) as well as that of electrons with \(v_{b}<v<v_{ac}\), which continues to decrease (dashed curve), meanwhile the densities of electrons with higher velocities significantly increase (curves 3 and 4 corresponding to velocity intervals “3” and “4”). This shows that the presence of a non negligible amount of accelerated electrons up to \((2-3)v_{b}\) is due to the SDC process.
The simulation results show that electron acceleration observed at large times results from damping of Langmuir waves \(\mathcal{L}^{\prime\prime}\) coming from the second decay cascade. It is useful to discuss such observations on the basis of available theoretical arguments and, in particular, the competition between the various physical processes at work during the full time evolution. The first one consists in the transfer of Langmuir wave energy to smaller \(k\)-scales due to the interactions of these waves with the plasma, that is, their scattering on the fluctuating density inhomogeneities (time scale \(\tau_{s}\)). Second, resonant wave-particle interactions govern the beam instability and the wave growth which can be described, in the frame of the weak turbulence theory for homogeneous plasmas, by quasilinear diffusion and spectral saturation (time scale \(\tau_{D}\)). Third, nonlinear wave-wave interactions occur in the form of resonant three-wave decay (time scale \(\tau_{2}\)), for which some analytical estimates can be provided by the turbulence theory; however, this concerns only limited aspects, as we know that decay is significantly affected by the presence of inhomogeneities constraining the interactions to be localized.
The time ordering necessary for an efficient acceleration of electrons by the \(\mathcal{L}^{\prime\prime}\) waves has been determined. The conditions \(\tau_{s}<\tau_{D}\) and \(\tau_{2}\lesssim\tau_{D},\) which fit with the theoretical estimates (Krafft and Volokitin, 2016) and the simulation results, require that the scattering processes are already saturated when the diffusion of the beam particles due to the waves \(\mathcal{L}^{\prime\prime}\) takes place \((\tau_{s}<\tau_{D})\), which is in turn evolving on a time scale of the order or larger than the duration of the energy transfer from the waves \(\mathcal{L}^{\prime}\) to the waves \(\mathcal{L}^{\prime\prime}\) (\(\tau _{2}\lesssim\tau_{D}\)). On the basis of these relations and the resonance conditions between the beam electrons and the Langmuir waves \(\mathcal{L}% ^{\prime\prime}\), one has determined that, for solar wind conditions typical of the type III solar bursts’ source regions and the Earth foreshock, electron beams with drift velocities in the range \(8v_{T}\lesssim v_{b}\lesssim35v_{T}\) can be the source of the acceleration process described here, by exciting Langmuir waves which in turn experience decay cascades and Landau damping.
Conclusions
Numerical simulation results and analytical estimates have shown that the process of electron acceleration by daughter Langmuir waves \(\mathcal{L}% ^{\prime\prime}\) coming from the second cascade \(\mathcal{L}^{\prime}\rightarrow\mathcal{L}^{\prime\prime}+\mathcal{S}^{\prime\prime}\) of the electrostatic decay \(\mathcal{L}\rightarrow\mathcal{L}^{\prime}+\mathcal{S}% ^{\prime}\) of Langmuir waves \(\mathcal{L}\) driven by an electron beam can occur at a significant level in solar wind regions where density fluctuations may exist, if the beam drift velocities \(v_{b}\) satisfy roughly the condition \(8v_{T}\lesssim v_{b}\lesssim35v_{T}.\) This range corresponds to the drift velocities of the beams actually existing in the solar wind regions of the foreshock and the type III solar bursts’ sources. Moreover, such process can be particularly efficient if beforehand scattering effects of Langmuir waves on the background plasma density inhomogeneities have already accelerated a sufficient amount of electrons. Then the Langmuir waves \(\mathcal{L}% ^{\prime\prime}\) produced by the second decay cascade can accelerate again these beam particles up to velocities and kinetic energies exceeding respectively two times the beam drift velocity \(v_{b}\) and half the initial beam energy. Note that the two acceleration processes at work, i.e. due to the scattering of waves on the density inhomogeneities and to the second decay cascade, do not occur in the same range of time, as the first one is already saturated when the rise of the second one becomes significant.
Additional info
This nugget is based on the paper
Krafft, C., & Volokitin, A. (2016). ELECTRON ACCELERATION BY LANGMUIR WAVES PRODUCED BY A DECAY CASCADE The Astrophysical Journal, 821 (2) DOI: 10.3847/0004-637X/821/2/99
Corresponding author : Catherine.krafft@lpp.polytechnique.fr
This work was granted access to the HPC resource of IDRIS under the allocation 2013- i2013057017 made by GENCI. This work has been done within the LABEX Plas@par project, and received financial state aid managed by the Agence Nationale de la Recherche, as part of the programme “Investissements d’avenir” under the reference ANR-11-IDEX-0004-02. C.K. acknowledges the “Programme National Soleil Terre” (PNST) and the Centre National d’Etudes Spatiales (CNES, France).
References
Ergun, R.E., Larson, D., Lin, R.P., et al. : 1998, ApJ, 503, 435
Graham, D.B., and Cairns, I.H.: 2013, J. Geophys. Res, 118, 3968
Kontar, E.P., Pecseli, H.L. : 2002, Phys. Rev., 65, 066408
Krafft C., Volokitin A.S., Krasnoselskikh, V.V. : 2015, ApJ, 809, 176
Krafft C., Volokitin A.S., Krasnoselskikh, V.V. : 2013, ApJ, 778, 111
Ryutov, D.D. : 1969, Sov. JETP, 30, 131